Does $\int_0^1 x^2 \sin(\pi x) x^x (1-x)^{1-x} \mathrm{d}x = \frac{73}{5760} \pi e$?

Question

A few months ago, I was looking through some integrals on AOPS and I came across this one.

• Finding it very interesting, I asked (on $7/24$) if any progress had been made on confirming or refuting its conjectured value but there has been no response.
• This integral is way over my level and I don't even know how to attempt solving this.
• My only ideas have to do with the $x^{x}\left(1 - x\right)^{1 - x}$ part reminding me of the sophomore's dream integral but I have no clue how to solve this.
• Does $$ \int_{0}^{1}x^{2}\sin\left(\pi x\right)\,x^{x} \left(1 - x\right)^{1 - x}\,\mathrm{d}x = \frac{73}{5760}\,\pi{\rm e}\ ? $$

Answer 1

Yes, it's true!

Let $x = \frac{1}{1+e^u}$ so that $dx = -\frac{1}{2\cosh u+2}\,du$. Then

$$ \begin{align} \mathcal{I} &:= \int_{0}^{1}x^{2}\sin\left(\pi x\right)x^{x}\left(1-x\right)^{1-x}\,dx \\ &= \int_{\mathbb{R}}\left(\frac{1}{e^{u}+1}\right)^{2}\sin\left(\frac{\pi}{e^{u}+1}\right)\left(\frac{1}{e^{u}+1}\right)^{\frac{1}{e^{u}+1}}\left(1-\frac{1}{e^{u}+1}\right)^{1-\frac{1}{e^{u}+1}}\frac{1}{2\cosh u+2}\,du \\ &= \int_{\mathbb{R}}\frac{e^{2u}}{\left(1+e^{u}\right)^{5}}\sin\left(\frac{\pi}{e^{u}+1}\right)\exp\left(-\frac{u}{e^{u}+1}\right)\,du \\ &= \Im\int_{\mathbb{R}}\frac{e^{2u}}{\left(1+e^{u}\right)^{5}}\exp\left(\frac{i\pi-u}{e^{u}+1}\right)\,du\,. \end{align} $$

Define a holomorphic function $f: \mathbb{C}\,\setminus \left\{(2k+1)\pi i:k\in\mathbb{Z}\right\} \longrightarrow \mathbb{C}$ where $z \mapsto \frac{e^{2z}}{\left(1+e^{z}\right)^{5}}\exp\left(\frac{i\pi-z}{1+e^{z}}\right)$. We also construct a counterclockwise contour in the shape of a rectangle $C = [-R,R]\cup\Lambda_1\cup\Lambda_2\cup\Lambda_3$, where

$$ \begin{align} \Lambda_1 &= \left\{R+it\in\mathbb{C}:t\in[0,2\pi]\right\} \\ \Lambda_2 &= \left\{2\pi i-t\in\mathbb{C}:t\in[-R,R]\right\} \\ \Lambda_3 &= \left\{-R-it\in\mathbb{C}:t\in[-2\pi,0]\right\}\,. \\ \end{align} $$

Feel free to click this link for an animation of what traveling around the contour looks like, using Desmos's new October 2024 update featuring complex numbers. Below is a visual of the contour with RGB domain coloring and shading.

$$\text{Figure 1: Rectangular Contour $C$ Traveling Positively}$$

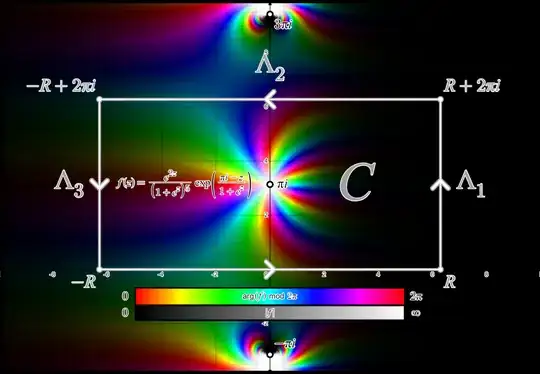
We write the contour integral over $C$ as the sum of integrals

$$ \oint_{C}f = \int_{-R}^R f + \int_{\Lambda_1}f + \int_{\Lambda_2}f + \int_{\Lambda_3}f\,. $$

We equate the imaginary part on both sides and apply $R \to \infty$ as

$$ \lim_{R\to\infty}\Im\oint_{C}f = \mathcal{I} +\lim_{R\to\infty}\Im\int_{\Lambda_1}f + \lim_{R\to\infty}\Im\int_{\Lambda_2}f + \lim_{R\to\infty}\Im\int_{\Lambda_3}f\,. $$

First, we will evaluate the integral over $\Lambda_1$ as $R \to \infty$. Bounding the modulus of the integral, we use the Triangle Inequalities and the equation $\left|e^w\right| = e^{\Re w}$ for all $w \in \mathbb{C}$ to get

$$ \begin{align} \left|\Im\int_{\Lambda_1}f(z)\,dz\right| &\leq \left|\int_{\Lambda_1}f(z)\,dz\right| \\ &\overset{t\in\Lambda_1}=\left|\int_{0}^{2\pi}f(R+it)i\,dt\right| \\ &=\left|\int_{0}^{2\pi}\frac{e^{2\left(R+it\right)}}{\left(1+e^{R+it}\right)^{5}}\exp\left(\frac{i\pi-\left(R+it\right)}{1+e^{R+it}}\right)\,dt\right| \\ &\leq \int_{0}^{2\pi}\left|\frac{e^{2\left(R+it\right)}}{\left(1+e^{R+it}\right)^{5}}\exp\left(\frac{i\pi-\left(R+it\right)}{1+e^{R+it}}\right)\right|\,dt \\ &\leq \int_{0}^{2\pi}\frac{e^{2R}}{\left(e^{R}-1\right)^{5}}\exp\left(\Re\left(\frac{i\pi-R-it}{1+e^{R}e^{it}}\right)\right)\,dt \\ &= \int_{0}^{2\pi}\frac{e^{2R}}{\left(e^{R}-1\right)^{5}}\exp\left(\frac{e^{R}t\sin t+\pi e^{R}\sin t-Re^{R}\cos t-R}{e^{2R}+2e^{R}\cos t+1}\right)\,dt\,. \end{align} $$

We have the inequality

$$ 0\leq\left|\Im\int_{\Lambda_1}f(z)\,dz\right|\leq\int_{0}^{2\pi}\frac{e^{2R}}{\left(e^{R}-1\right)^{5}}\exp\left(\frac{e^{R}t\sin t+\pi e^{R}\sin t-Re^{R}\cos t-R}{e^{2R}+2e^{R}\cos t+1}\right)\,dt\,. $$

Notice that

$$ \lim_{R\to\infty}\int_{0}^{2\pi}\frac{e^{2R}}{\left(e^{R}-1\right)^{5}}\exp\left(\frac{e^{R}t\sin t+\pi e^{R}\sin t-Re^{R}\cos t-R}{e^{2R}+2e^{R}\cos t+1}\right)\,dt\, = \int_{0}^{2\pi}0\cdot\exp\left(0\right)\,dt = 0\,. $$

Using the Squeeze Theorem, we get

$$ \lim_{R\to\infty}\left|\Im\int_{\Lambda_1}f(z)\,dz\right| = 0 $$

which implies

$$ \lim_{R\to\infty}\Im\int_{\Lambda_1}f(z)\,dz = 0\,. $$

The integral over $\Lambda_3$ follows a similar but more tedious procedure. I'll leave it up to you to evaluate it.

Next, we recover the desired integral $\mathcal{I}$ by manipulating the integral over $\Lambda_2$ like

$$ \begin{align} \int_{\Lambda_2}f(z)\,dz &\overset{t\in\Lambda_2}=\int_{-R}^Rf(-t+2\pi i)(-1)\,dt \\ &\overset{-t=x}= \int_{R}^{-R}f(x+2\pi i)\,dx \\ &= -\int_{-R}^{R}\frac{e^{2\left(x+2\pi i\right)}}{\left(1+e^{x+2\pi i}\right)^{5}}\exp\left(\frac{i\pi-\left(x+2\pi i\right)}{e^{x+2\pi i}+1}\right)\,dx \\ &= -\int_{-R}^{R}\frac{e^{2x}}{\left(1+e^{x}\right)^{5}}\exp\left(-\frac{x}{e^{x}+1}\right)\exp\left(-\frac{\pi i}{e^{x}+1}\right)\,dx\,. \\ \end{align} $$

Equating the imaginary part and applying $R \to \infty$ on both sides, we get

$$ \lim_{R\to\infty}\Im\int_{\Lambda_2}f(z)\,dz = -\lim_{R\to\infty}\int_{-R}^{R}\frac{e^{2x}}{\left(1+e^{x}\right)^{5}}\exp\left(-\frac{x}{e^{x}+1}\right)\sin\left(-\frac{\pi}{e^{x}+1}\right)\,dx = \mathcal{I}\,. $$

Next, we evaluate the integral over the entire contour using the Residue Theorem. First, there is a fifth-order pole at $z=\pi i$ (the rainbow hue in the screenshot "goes around" five times for lack of a better term) and essential singularities at $z = (2k+1)\pi i$ for all integers $k$ besides $k=0$. Regarding the fifth-order pole, we can redefine $\frac{i\pi-z}{1+e^z}$ as its power series representation

$$ \frac{i\pi-z}{1+e^z} = \sum_{n=0}^{\infty}\frac{B_n}{n!}(z-i\pi)^n = 1-\frac{1}{2}\left(z-i\pi\right)+\frac{1}{12}\left(z-i\pi\right)^{2}-\frac{1}{720}\left(z-i\pi\right)^{4}+\mathcal{O}\left(\left(z-i\pi\right)^{6}\right)\,, $$

where $B_n$ is the $n$th Bernoulli number. Using this, we see that plugging in $i\pi$ into $\frac{1}{f}$ yields

$$ \frac{1}{f(i\pi)} = \frac{\left(1+e^{i\pi}\right)^{5}}{e^{2\left(i\pi\right)}\exp\left(1-\frac{1}{2}\left(i\pi-i\pi\right)+\frac{1}{12}\left(i\pi-i\pi\right)^{2}-\frac{1}{720}\left(i\pi-i\pi\right)^{4}+\mathcal{O}\left(\left(i\pi-i\pi\right)^{6}\right)\right)} = 0\,, $$

which makes $z=i\pi$ a fifth-order pole of $f$. Though it's technically possible to use the Residue at Multiple Pole Theorem to evaluate the residue at $z = i\pi$, it would be so much differentiating and calculating. Instead, I decided to go with WolframAlpha's Laurent asymptotic series representation of $f$ and find the coefficient of $\frac{1}{z-i\pi}$ from the series:

$$ f(z) = -\frac{e}{\left(z-i\pi\right)^{5}}+\frac{e}{\left(z-i\pi\right)^{4}}-\frac{3e}{8\left(z-i\pi\right)^{3}}+\frac{e}{24\left(z-i\pi\right)^{2}}+\frac{73e}{5760\left(z-i\pi\right)}-\frac{5e}{1152}+\frac{299e\left(z-i\pi\right)}{2903040}+\frac{89e\left(z-i\pi\right)^{2}}{580608}-\frac{9949e\left(z-i\pi\right)^{3}}{464486400}+\mathcal{O}\left(\left(z-i\pi\right)^{4}\right)\,. $$

By Cauchy's Residue Theorem, we get

$$ \oint_{C}f(z)\,dz = 2\pi i\mathop{\mathrm{Res}}_{z=i\pi}f(z) = \frac{146\pi ei}{5760}\,. $$

Gathering all of the results together, we have

$$ \require{cancel}{\lim_{R\to\infty}\Im \frac{146\pi ei}{5760} = \mathcal{I} + \cancelto{0}{\lim_{R\to\infty}\Im\int_{\Lambda_1}f} + \mathcal{I} + \cancelto{0}{\lim_{R\to\infty}\Im\int_{\Lambda_3}f}}\,. $$

We end with

$$ \bbox[13px,#f1ffff ,border:5px double #a300ab ]{\int_{0}^{1}x^{2}\sin\left(\pi x\right)x^{x}\left(1-x\right)^{1-x}dx=\frac{73\pi e}{5760}} $$

and we're done! :)

Answer 2

Too long for a comment.
The other answer really did impressive work on this elusive integral. In addition to it, we want to find the inner structure of such integrals, and yield some more general results.

---

How to Integrate?
We can find the following function that works $$ f(z)=\frac{1}{z^k}\exp\left ( a\frac{\log(z-1)-\pi i}{z} \right ),\qquad k\in\mathbb{Z}_{\ge2} $$ where $\log(z)=\ln\left | z \right | +i\arg(z),\arg(z)\in[0,2\pi)$ is the logarithm of the principal branch. Noticing the function avoids the essential singularity at $z=0$ and as $z$ tends to infinity the function grows not so fast, we may simply integrate it along a keyhole contour with branch cut $(1,\infty)$, which gives $$ \int_{1}^{\infty} \frac{1}{z^k} \exp\left (a \frac{\ln(z-1)}{z} \right ) \sin\left ( a\frac{\pi}{z} \right ) \text{d}z =-\pi [\operatorname{Res}(f,0)+\operatorname{Res}(f,1)]. $$ In conclusion, $$ \int_{0}^{1}z^{k-2} \left [ z^{-z}(1-z)^z \right ]^a\sin\left ( a\pi z \right ) \text{d}z=-\pi[\operatorname{Res}(f,0)+\operatorname{Res}(f,1)]. $$ The questioned integral is done by evaluating the following two integrals, where I used Wolfram Alpha to calculate those residues: $$ \begin{aligned} &\int_{0}^{1}x^{2} x^{x}(1-x)^{-x}\sin\left ( \pi x \right ) \text{d}x = \frac{7\pi e}{16} -\pi,\\ &\int_{0}^{1}x^{3} x^{x}(1-x)^{-x}\sin\left ( \pi x \right ) \text{d}x = \frac{2447\pi e}{5760} -\pi. \end{aligned} $$

---

How to Generalize?
Here are some ways to generalize the result. They're in abundance. For direct generalizations, one may evaluate $$ \int_{0}^{1} R(x)\left [ x^{-x}\left ( 1-x \right )^{-x} \right ]^a \sin\left( a\pi x \right) \text{d}x $$ where $R(x)$ is a rational function whenever the value exists. And the crucial point of our function is to avoid the essential singularity at $z=0$. From this aspect we may consider integrating for $p\in\mathbb{N}$, $$ f(z)=\frac{1}{z^k} \exp\left [ \frac{a}{z^{p}} \left ( \log(z-1)-\pi i+\sum_{n=1}^{p-1} \frac{z^n}{n} \right) \right ]. $$ For instance, setting $p=7$ gives this almost impossible integral: $$ \int_{0}^{1} e^{-\left ( x^6+\frac{x^5}{2}+\frac{x^4}{3} +\frac{x^3}{4} +\frac{x^2}{5} +\frac{x}{6}\right ) } x^{x^7}(1-x)^{1-x^7}\sin\left ( \pi x^7 \right ) \text{d}x=\frac{7\pi\sqrt[7]{e} }{1152}. $$ Another important point is the branch property of our functions. Integrating the dilogarithm $\operatorname{Li}_2$, $$ f(z)=\frac{1}{z^k}\exp\left ( a\frac{\operatorname{Li}_2(z)}{z} \right ), $$ one have this disgusting integral after substituting $\ln x\to e^{-x}$: $$ \int_{0}^{\infty} \frac{\sin(\pi xe^{-x})}{\cosh(x)} \exp\left({{ -e^{-x} \left ( \frac{\pi^2}{3} -\frac{x^2}{2} -\operatorname{Li}_2(e^{-x}) \right )}}\right)\text{d}x =2\pi e^{-G}\sin\left ( \frac{\pi^2}{48} \right ), $$ where $G=\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^2}$ denotes Catalan's constant.

Answer 3

The integral was posted by me on AoPS. There’s someone named Brian J. Diaz who actually showed me the integral first, and I asked them for a solution. What they posted is shown below. This was a long time ago, so there might be a research paper available by now

If this isn’t helpful, just let me know in the comments and I’ll delete it

I will be a publishing a paper on this in arXiv.org, but I think that will be as far as my pursuit will go. This is something I am absolutely cautious to share, but I feel the need unveil anyway. I have lost some will to believe this is a significant result due to doubts expressed by other mathematicians who I have corresponded with, so this led me to construe this might not be important after all. I have read about these integrals supposedly popping up in the work of Ramanujan, though I have found no reliable source, and Bruce Berndt still has yet to get back to me. :(

This project started when I was curious what parametrizations would be needed to encapsulate impressive information about the following integrals:

\begin{align} &\int_0^1 \sin(\pi x) x^x(1-x)^{1-x} \, dx &= \frac{\pi e}{24} \\ &\int_0^1 \frac{\sin(\pi x)}{x^x(1-x)^{1-x}}\, dx &= \frac{\pi }{e} \\ &\int_0^1 \frac{\sin(\pi x)}{x(1-x)}\frac{1}{x^x(1-x)^{1-x}}\, dx &= 2\pi \end{align}

However, as it turns out, I was able to show they are related via the following theorem.

$\textbf{Theorem}$ For $m, q \in \mathbb{Z}$, and $m+q+1 \geq 0$, $$ \int_0^1 x^m \sin\left(\pi q x \right) \left(x^x (1-x)^{1-x}\right)^q\ dx = (-1)^{q+1} \frac{d_{m+q+1}(q)}{(m+q+2)!_\mathbb{P}} \pi e^{q}$$ where $d_n(q)$ is a primitive polynomial of $\mathbb{Z}[x]$ of degree $n$, and $ n!_\mathbb{P}$ is the Bhargava factorial over the set of primes.

In addition, these rational numbers satisfy a neat recurrence relation, of which Carleman's inequality is a [special case][1] of:

$$\frac{d_{n}(q)}{(n+1)!_\mathbb{P}} = -\frac{q}{n} \sum_{k=1}^n \frac{d_{n-k}(q)}{(n-k+1)!_\mathbb{P}} \frac{1}{k+1}; \; d_0(q) = -1,\; \text{if} \,(q\neq 0).$$

Using these results, we can unlock a whole class of crazy stuff:

\begin{align*}\sum_{j=1}^n A_j(1-\alpha_j)^{q\left(1-\frac{1}{\alpha_j}\right)}&= (-1)^q\int_0^1 \frac{\sin\left(\pi q x \right)}{\pi x} \frac{\left[x^x\left(1-x\right)^{1-x}\right]^q}{x^q} \prod_{j=1}^n \frac{1}{1-\alpha_j x}\ dx, \end{align*} \begin{align*} A_j = \prod_{k=1, k\neq j}^n \frac{\alpha_j}{\alpha_j-\alpha_k}, \quad \alpha_j \in (0,1). \end{align*}

Here are some special values: \begin{align} &\int_0^1 \frac{\sin\left( \pi x \right)}{ (1-x)\left[x^x\left(1-x\right)^{1-x}\right]} \ dx = \pi \quad \quad &\int_0^1 \frac{\sin\left( \pi x \right)}{(1-x^2)\left[x^x\left(1-x\right)^{1-x}\right]} \ dx &= \frac{5\pi}{8} \end{align}

I don't want to reveal too much anyway. Enjoy! [1]: https://www.people.fas.harvard.edu/~sfinch/csolve/crl.pdf (Use wayback machine)