Maximizing the angle subtended by the foci of the ellipse $4x^2+13y^2=52$ at a point on the line $2x+y=12$

Question

Consider the ellipse E: $4x^2+13y^2=52$. Let P be a point on the line L: $2x+y=12$ such that the foci of the ellipse subtend maximum angle at P. Find the ratio of the distances of P from the foci of ellipse.

My method- I took a circle passing through the foci and touching the given line. The point of contact is P as a chord subtends greater angle at at circumference than any point outside, then I solved the point P and then used distance formula.

I got the answer but it was too lengthy.

Does anyone have any approach using any properties? (As it is expected from me to solve this in max 5 mins in a exam)

Answer 1

Let $A=(3,0)$, $B=(-3,0)$ be the foci of the ellipse, and $E=(6,0)$ the intersection point between line $L$ and $x$-axis. From power of point $E$ with respect to circle $PAB$ (which is tangent to $L$, as you observed) we get at once: $$ PE=\sqrt{EA\cdot EB}=3\sqrt3. $$ On the other hand we have (tangent-chord theorem in circle $PAB$): $$ \angle PBA=\angle APE. $$ Hence, by the sine law applied to triangles $APB$ and $APE$ we get: $$ {PB\over PA}={\sin \angle PAB\over\sin \angle PBA}= {\sin \angle PAE\over\sin \angle APE}={PE\over AE}= {3\sqrt3\over3}=\sqrt3. $$

Answer 2

Here is a solution giving all the details, yes, it is too much for the five minutes, but only because we have annoying computations in $\Bbb Q(\sqrt{15})$. Up to this fact the steps are easy...

---

The elipse has the equation: $$E\ :\qquad \left(\frac x{\sqrt{13}}\right)^2+ \left(\frac y2\right)^2 =1\ . $$ So it passes through the points $(\pm a,0)$ with $a=\sqrt 13$, and $(0,\pm b)$ with $b=2$. Since $0<b<a$ the focal points are of the shape $F_\pm=(\pm f,0)$, lying on the axis with the maximal distance between two ellipse points. Applying the geometric property for the points $(a,0)$, $(0,b)$ (sum of distances to the foci is the same one) we obtain the equality of $(a-f)+(a+f)$ (sum of distances from $(a,0)$ to the foci $F_\pm=(\pm f,0)$) and $2\sqrt{f^2+b^2}$ (sum of distances from $(0,b)$ to the foci $F_\pm=(\pm f,0)$). This gives $f=3$. From this point we can forget about the ellipse. So far all the computations can be done without paper.

---

We need now the point on the line $L$ with equation $2x+y=12$ so that the circle through $P$ and the foci is tangent to $L$. By symmetry, its center $\Omega$ is on the perpendicular bisector of the segment between the foci, so it is on $Oy$. Let $\Omega=(0,t)$, be this point. Its distance to the foci is $\sqrt{3^2+t^2}$. The formula for this distance leads to: $$ \sqrt{t^2+3^2}=\frac{|2\cdot 0+t-12|}{\sqrt{2^2+1^2}}\ . $$ So $5t^2+45=t^2-24t+144$, so $4t^2+24t-99=0$. So $t=-3\pm \frac 32\sqrt{15}$. For geometric reasons we keep only the $t$ with the plus sign.

---

---

The projection of $0$ on the line $L$ is the point on $L$ and the line through the origin with slope $2/1$, so it is a point of the shape $(2s,s)$ and we quickly obtain $s$. We know the position of $\Omega$ between $(0,12)$ and the origin.

It is $\displaystyle(0,12)+\alpha((0,0)-(0,12))$. Here, $\alpha=\frac 18(10-\sqrt {15})$.

So the point $P$, projection of $\Omega$ on $L$ is: $$ P= \displaystyle(0,12)+\alpha \left(\left(\frac{24}5,\frac{12}5\right)-(0,12)\right) = \frac 35(10-\sqrt {15},\ 2\sqrt{15})\ . $$

---

We need a proportion of sides in the triangle $PF_-F_+$. It is the same proportion if we are using the scaling factor $5/3$. So we consider the points $P'=(10-\sqrt {15},\ 2\sqrt{15})$, $F'_\pm=(\pm 5,0)$ and work with them instead: $$ \begin{aligned} \overrightarrow{F_-'P'}=P'-F_-' &=(15-\sqrt {15},\ 2\sqrt{15})=\sqrt{15}(\sqrt{15}-1, 2)\ , \\ \overrightarrow{F_+'P'}=P'-F_+' &=(5-\sqrt {15},\ 2\sqrt{15})\ , \\ |F_-'P'|^2 &=15(20-2\sqrt{15})=30(10-\sqrt{15})\ , \\ |F_+'P'|^2 &=(100-10\sqrt{15})=10(10-\sqrt {15})\ ,\qquad\text{ and we obtain} \\ \frac{|F_-P|}{|F_+P|}= \frac{|F_-'P'|}{|F_+'P'|} &=\sqrt 3\ . \end{aligned} $$

---

Answer 3

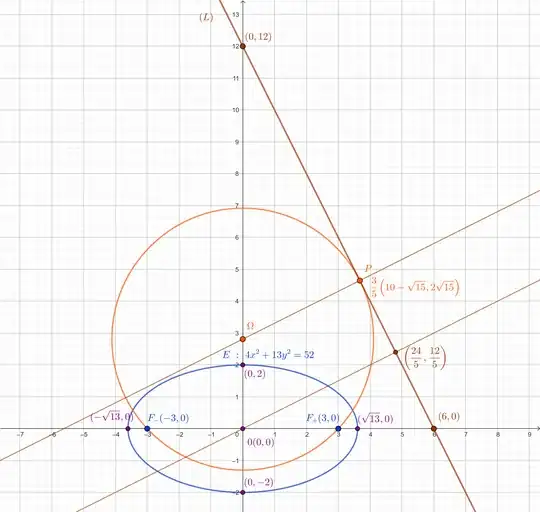
Let us put the equation of the ellipse under its canonical form :

$$\frac{x^2}{(\sqrt{13})^2}+\frac{y^2}{2^2}=1\tag{1}$$

Therefore, the abscissas of its foci are $f=\pm \sqrt{a^2-b^2}=\pm 3$.

A recall : the locus of points "seing" a same segment (here $FF'$) under a same (non-oriented acute) angle $\theta$ is the curve $C_{\theta}$ which is the union of 2 circular arcs as represented here connected in points $F,F'$. These curves are "embedded" like russian dolls. The smaller the angle, the larger the curve. We are looking here for the larger value of $\theta$ for which curve $C_{\theta}$ is tangent to line $L$.

Have a look at the figure below featuring the two points on the line which are the two extremal solutions :

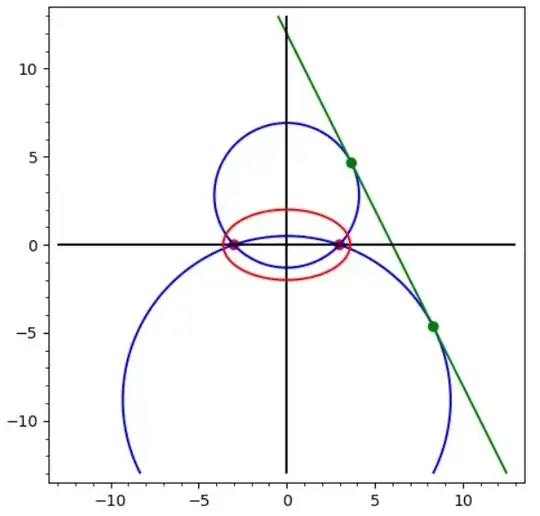
Fig.1 : The two points (green dots) which are extremal solutions. Strictly speaking, it is the upper one which exhibits the larger angular value.

Here is a description of the way these points have been obtained :

• Step 1: It is not difficult to see that the generic equation of the circles passing through both foci $F(-3,0)$ and $F'(3,0)$ is

$$x^2+y^2-2dx-9=0\tag{2}$$

where the center of the circle is in $(0,d)$

(such a set of circles is called an "elliptical pencil of circles")

• Step 2 : You probably know the classical rule giving the equation of the tangent of a circle with an equation like (2) in a point $(x_0,y_0)$ is by polarizing it (I will look for a hopefuly more convenient term in English) in the following way :

$$xx_0+yy_0-d(y+y_0)-9=0$$

(sanity check : suppressing indices $_0$, one finds back equation (2).)

Otherwise said :

$$xx_0+y(y_0-d) -(dy_0+9)=0$$

• Step 3 : the former equation is eqivalent to the given equation $2x+y-12=0$ iff their coefficients are proportional:

$$\frac{x_0}{2}=\frac{y_0-d}{1}=\frac{dy_0+9}{12}\tag{3}$$

As $(x_0,y_0)$ belongs to line $L$, i.e., we have as well :

$$2x_0+y_0-12=0\tag{4}$$

• Step 4: Equations (3)+(4) constitute a system of 3 equations with 3 unknowns ; it is not difficult to solve it ; here are the two solutions (with the coordinates $(x_0,y_0)$ of the points and the ordinates $d$ of the centers of the corresponding circles (where we have set $k=\sqrt{15}$).

$$\begin{cases}x_0& =& -(3/5)k + 6, \ \ \ \ &y_0 &=& +(6/5) k, \ \ \ \ &d &=& +(3/2) k - 3 \\ x_0 &=& +(3/5)k + 6, \ \ \ \ &y_0 &=& -(6/5) k, \ \ \ \ &d &=& -(3/2) k - 3 \end{cases}$$

As said in the legend of Fig. 1, only the first point should be finally considered.

• Step 5: Once the coordinates of the optimal point $P_0$ have been obtained, it is easy to compute the ratio $P_0F/P_0F'$ ; one finds $\sqrt{3}$.

For those who are interested in the way the figure has been drawn, here is its "Sage" program :

 var('x y d')
 s=solve([2*x+y==12,x/2==y-d,y-d==(d*y+9)/12],x,y,d)
 x0=s[0][0].rhs();y0=s[0][1].rhs();
 x1=s[1][0].rhs();y1=s[1][1].rhs();
 print(s)
 L=13
 g=line([(-L,0),(L,0)],color='black')
 g+=line([(0,-L),(0,L)],color='black')
 d=s[0][2].rhs();g+=implicit_plot(x^2+y^2-2*d*y-9==0,(x,-L,L),(y,-L,L))
 d=s[1][2].rhs();g+=implicit_plot(x^2+y^2-2*d*y-9==0,(x,-L,L),(y,-L,L))
 g+=implicit_plot(2*x+y==12,(x,-L,L),(y,-L,L),color='green')
 g+=implicit_plot(x^2/13+y^2/4==1,(x,-L,L),(y,-L,L),color='red')
 g+=point(((-3,0),(3,0)),color='red',size=50)
 g+=point(((x0,y0),(x1,y1)),color='green',size=50)
 show(g)