Continuous approximations to classic distributions: some properties verification

Question

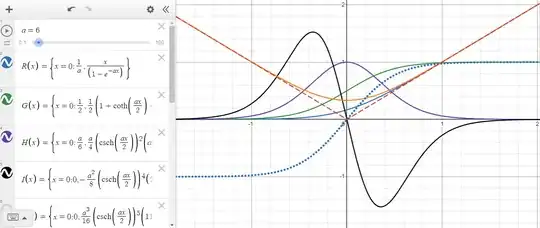
On previous question and answer I realized that the following function could make an easy continuous approximation for the ramp function, and reviewing it later, I also realize it could also approximate many of the classic distributions, electricians like me, use as they were functions:

1. The Ramp function $R(x)$ could be approximated by $$\mathring{R}(x):\approx \lim_{\varepsilon\to\infty}\begin{cases}\dfrac{1}{\varepsilon},\quad x=0\\ \dfrac{x}{1-e^{-\varepsilon x}}=\dfrac{x}{2}\left(1+\coth\left(\dfrac{\varepsilon x}{2}\right)\right),\,x\neq 0\end{cases}$$
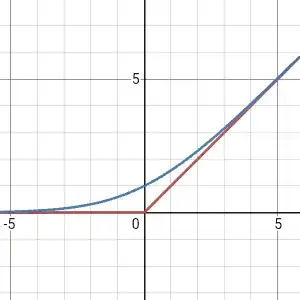
2. The Heaviside step function $\theta(x)$ could be approximated by $\mathring{R}'(x)$ as: $$\mathring{\theta}(x) :\approx \lim_{\varepsilon\to\infty}\begin{cases}\dfrac{1}{2},\quad x=0\\ \dfrac{1}{2} \left(1+\coth\left(\dfrac{\varepsilon x}{2}\right)-\dfrac{\varepsilon x}{2}\text{csch}^2\!\left(\dfrac{\varepsilon x}{2}\right)\right),\,x\neq 0\end{cases}$$
3. The Dirac's Delta function $\delta(x)$ could be approximated by $\mathring{R}''(x)$ as: $$\mathring{\delta}(x) :\approx \lim_{\varepsilon\to\infty}\begin{cases}\dfrac{\varepsilon}{6},\quad x=0\\ \dfrac{\varepsilon}{4}\, \text{csch}^2\!\left(\dfrac{\varepsilon x}{2}\right)\!\left(\varepsilon x\coth\left(\dfrac{\varepsilon x}{2}\right)-2\right) ,\,x\neq 0\end{cases}$$
4. Also $\delta'(x)$ could be approximated by $\mathring{R}^{(3)}(x)$ as: $$\mathring{\delta\delta}(x) :\approx \lim_{\varepsilon\to\infty}\begin{cases}0,\quad x=0\\ -\dfrac{\varepsilon}{8}\, \text{csch}^4\!\left(\dfrac{\varepsilon x}{2}\right)\!\bigg(2\varepsilon x+\varepsilon x\cosh\left(\varepsilon x\right)-3\sinh\left(\varepsilon x\right)\bigg) ,\,x\neq 0\end{cases}$$
5. The Absolute value could be approximated by $2\mathring{R}(x)-x$ as: $$\mathring{A}(x):\approx \lim_{\varepsilon\to\infty}\begin{cases}\dfrac{2}{\varepsilon},\quad x=0\\ x\coth\left(\dfrac{\varepsilon x}{2}\right),\,x\neq 0\end{cases}$$
6. And finally, the Sign function could be approximated by $\mathring{A}'(x)$ as: $$\mathring{S}(x) :\approx \lim_{\varepsilon\to\infty}\begin{cases}0,\quad x=0\\ \coth\left(\dfrac{\varepsilon x}{2}\right)-\dfrac{\varepsilon x}{2}\text{csch}^2\!\left(\dfrac{\varepsilon x}{2}\right),\,x\neq 0\end{cases}$$

If I didn't messed it up, as the original functions, their approximations fulfills:

• $\mathring{S} =2\mathring{\theta}(x)-1$ follows $\text{sgn}(x) = 2\theta(x)-1$
• $\frac{d}{dx}\mathring{S}(x) = 2\mathring{\delta}(x)$ follows $\frac{d}{dx}\text{sgn}(x)=2\delta(x)$
• $\mathring{A} =2\mathring{R}(x)-x$ follows $|x| = 2R(x)-x$

But now, the following is not true: $\frac{\mathring{A}(x)}{x} \neq \frac{|x|}{x}=\text{sgn}(x)$ since $\frac{\mathring{A}(x)}{x}\neq \mathring{S}(x)$

What I liked about them is that even they have primitives in closed form, and I could made all of them from $\mathring{R(x)}$ using simple operations like addition and differentiation which are simple for working with them in the Fourier domain. So, using the definition of $\mathring{A}(x)$ I am trying to find all their Fourier transforms.

From Wolfram-Alpha the transform is given by: $$\mathbb{F}\{\mathring{A}(x)\}(w) := \int\limits_{-\infty}^\infty x\coth\left(\dfrac{\varepsilon x}{2}\right)e^{-iwx} dx = -\pi\left(\frac{\text{csch}\!\left(\frac{\varepsilon w}{2}\right)}{\varepsilon}\right)^2$$

Questions:

1. Are the approximation functions $1-6$ smooth $C^\infty$? (as example, like how this example is a smooth approximation of $\theta(x)$)
2. Which differential equation is fulfilled by $\mathring{A}(x)$?
3. Is the Fourier Transform $\mathbb{F}\{\mathring{A}(x)\}(w)$ well obtained? I am worried about the piecewise definition at $x=0$, as also as $\varepsilon\to\infty$ it don't follows $\mathbb{F}\{\mathring{|x|}\}(w) = -\dfrac{1}{\pi w^2} $ (looks closer when $\varepsilon \approx 1$ than when $\varepsilon \to \infty$ where the transform almost goes to zero, is closer to $-\delta(x)$).
4. Could be possible to found for real-values $t_0<t_f$ the following Fourier Transform in a finite interval?: $$ \mathbb{F}\{\mathring{A}(x)\}(w)\Biggr|_{t_0}^{t_f} := \int\limits_{t_0}^{t_f} x\coth\left(\dfrac{\varepsilon x}{2}\right)e^{-iwx} dx$$

Main Objective

I am trying to find a way to solve this another question using the convolution property of the Fourier Transform and later making $\varepsilon \to \infty$ to see which terms holds on the formulas.

Here a plot of the approximations in Desmos:

Answer 1

If your goal is to regularize those functions I will share an alternative (perhaps simpler) approach: $$ \begin{align} \delta_\epsilon(x) &= \frac{\text{sech}^2( x/\epsilon)}{2\epsilon} \\ H_\epsilon(x) &= 1+\frac{\text{tanh}( x/\epsilon)}{2} \\ \text{sgn}_\epsilon(x) &= \tanh(x/\epsilon) \\ R_\epsilon(x) &= \frac{x+\epsilon\ln(2\cosh(x/\epsilon))}{2} \\ \text{abs}_\epsilon(x) &= \epsilon\ln(2\cosh(x/\epsilon)) \end{align} $$ They all converge to the desired functions when $\epsilon\to0$. Furthermore, you have the usual relationship: $$ R_\epsilon’=H_\epsilon \quad \text{abs}_\epsilon’=\text{sgn}_\epsilon \quad \text{sgn}_\epsilon=2H_\epsilon-1 \quad H_\epsilon’=\delta_\epsilon $$ By direct inspection, all the functions are smooth.

The Fourier transforms are also pretty standard. Using the convention: $$ f(x)=\int\hat f(\xi)e^{i2\pi\xi x}d\xi \quad \hat f(x)=\int f(x)e^{-i2\pi\xi x}dx $$ You get: $$ \begin{align} \hat{\delta_\epsilon}(\xi) &= \frac{\pi\epsilon\xi}{2}\text{csch}(\pi\epsilon\xi/2) \\ \hat{H_\epsilon}(\xi) &= \frac{\epsilon}{4i}\text{csch}(\pi\epsilon(\xi-i\eta)/2) \\ \hat{\text{sgn}_\epsilon}(\xi) &= \frac{\epsilon}{4i}PV\text{csch}(\pi\epsilon\xi/2) \\ \hat{R_\epsilon}(\xi) &= -\frac{\epsilon}{8\pi(\xi-i\eta)}\text{csch}(\pi\epsilon(\xi-i\eta)/2) \\ \hat{\text{abs}_\epsilon}(x) &= -PV\frac{\epsilon}{8\pi\xi}\text{csch}(\pi\epsilon\xi/2) \end{align} $$ with $\eta\to0^+$.

Note that no matter the regularization, you will never have both: $$ R_\epsilon’=H_\epsilon \quad R_\epsilon=xH_\epsilon $$ Indeed the only solution to: $$ xy’=y $$ with $y(0)=0$ is $R$.