Geometry Problem on Congruent Triangles and Angle Chasing

Question

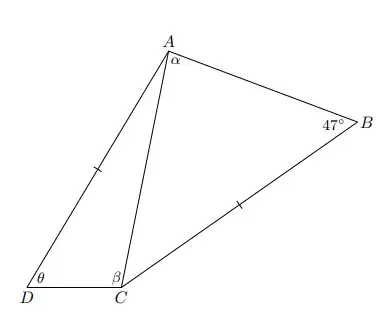
Okay so the question is: In the diagram below, $\overline{\text{AD}} \cong \overline{\text{BC}}$ and $\alpha + \beta = 180^\circ$ (diagram not to scale). Find the measure of $\theta$. We also get this information. Hint: First extend $\overline{\text{DC}}$ past C to the point E where $\overline{\text{CE}} \cong \overline{\text{AB}}$, then draw $\overline{\text{AE}}$ and look for congruent triangles.

We are given this picture:

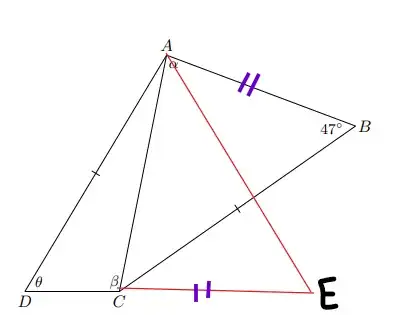
So first I extended $\overline{\text{DC}}$ to the right and made the new line segment be the same size as $\overline{\text{AB}}$. Then I drew a line down from point "A" to make a new triangle. This new point I called "E".

Now I wrote down what I know up to this point.

AD = BC, $\alpha + \beta = 180^\circ$ (we know because of Alternate (interior) angles) $\beta$ + $m\angle$ECA = 180$^\circ$ (we know this because angles on a straight line have to equal 180 degrees)

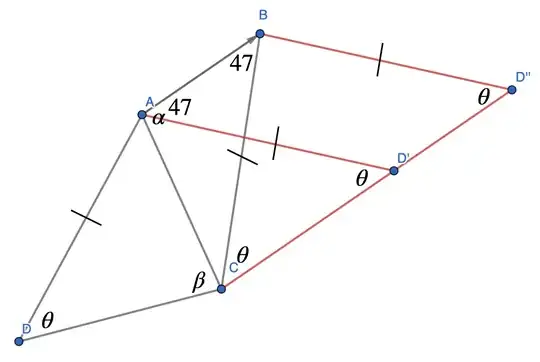
So this is where I get stuck on. I think I am supposed to focus on $\angle$BCA but I am not sure as to how I continue from here. Help would be very much appreciated! Thanks in advance!!

Answer 1

You've made a good start. As you noted, $\alpha + \beta = 180^{\circ}$ and $\beta + \measuredangle ECA = 180^{\circ}$, so comparing these $2$ equations gives

$$\measuredangle ECA = \alpha$$

Since $\lvert CE\rvert = \lvert AB\rvert$, by construction, and of course $\lvert CA\rvert = \lvert AC\rvert$, then by $SAS$ (Side-Angle-Side), we get

$$\triangle CEA \cong \triangle ABC$$

Thus, we also have

$$\measuredangle CEA = \measuredangle ABC = 47^{\circ}, \;\; \lvert EA\rvert = \lvert BC\rvert = \lvert AD\rvert$$

This means that $\triangle ADC$ is isosceles, and therefore

$$\theta = \measuredangle ADE = \measuredangle CEA = 47^{\circ}$$

---

Note that another way to determine this, with just the original diagram, is to use the law of sines. In $\triangle ACD$, we get

$$\frac{\sin(\measuredangle ACD)}{\lvert AD\rvert} = \frac{\sin(\measuredangle ADC)}{\lvert AC\rvert} \;\;\to\;\; \frac{\sin(\beta)}{\lvert AD\rvert} = \frac{\sin(\theta)}{\lvert AC\rvert}$$

while using this law in $\triangle ABC$ gives that

$$\frac{\sin(\measuredangle BAC)}{\lvert BC\rvert} = \frac{\sin(\measuredangle ABC)}{\lvert AC\rvert} \;\;\to\;\; \frac{\sin(\alpha)}{\lvert BC\rvert} = \frac{\sin(47^{\circ})}{\lvert AC\rvert}$$

Since $\alpha + \beta = 180^{\circ}$, then $\sin(\beta) = \sin(\alpha)$, and it's given that $\lvert AD\rvert = \lvert BC\rvert$, so comparing the above $2$ sets of equations results in

$$\sin(\theta) = \sin(47^{\circ})$$

Thus, we have either that $\theta = 47^{\circ}$ or $\theta + 47^{\circ} = 180^{\circ}$. However, in the latter case, this gives

$$\theta + 47^{\circ} = \beta + \alpha = 180^{\circ} \;\;\to\;\; (\theta + \beta) + (47^{\circ} + \alpha) = 360^{\circ}$$

Since the internal angles in a triangle sum to $180^{\circ}$, we also get

$$(\theta + \beta + \measuredangle CAD) + (47^{\circ} + \alpha + \measuredangle ACB) = 360^{\circ}$$

Comparing these $2$ sets of equations gives that

$$\measuredangle CAD + \measuredangle ACB = 0^{\circ}$$

which is impossible in non-degenerate triangles. Thus, we get, as before, that $\theta = 47^{\circ}$.

Answer 2

Reflect $AD$ about $AC$ to $AD'$ so $CD' \parallel AB$, translate $AD'$ by $AB$ to $BD''$ then we have isosceles $CBD''$ and $\theta=47$.

Edit: adding a bit about the logic of solving this problem. If you're given angles summing to $180$ the situation is ripe for two things, either getting those angles on a single line as supplements (what your hint did) or getting a set of parallel lines going (what I did by reflection). Since you are given two equal sides, it seems an isosceles triangle or a parallelogram would be helpful. Your hint shortcuts the isosceles approach (extend $AB, CE$, they meet, draw at $B$ a segment $BE \parallel AC$ and by Thales you have $AB=CE$) and John then uses triangle congruence on the shared base to get the result. The other approach, building parallel lines, is ready-made for generating parallelograms, which is what I did by translation. Which then gave me isosceles triangles where I needed them. Both of these are natural solutions to the situation.