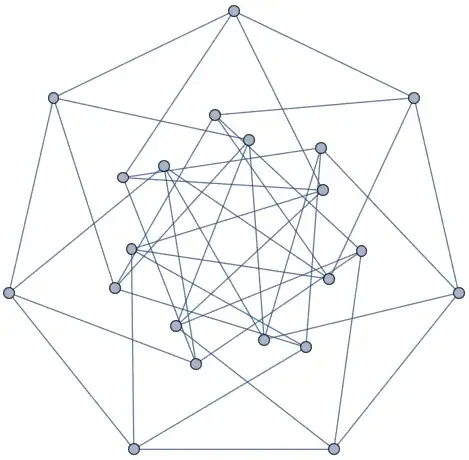
I earlier asked if this heptagon was rigid. Turned out, it is. In fact, it's so rigid that any two connected vertices can be removed with all edges and the resulting graph is still rigid. The link in this sentence shows other braced polygons (also Mathworld).
Let's call that property super-braced. The case for the Heptagon is solved, there it is above. What about simpler polygons: triangle, square, pentagon and hexagon with unit-length edges? What is the simplest super-braced version of these polygons? What is the minimal number of unit-length braces so that the graph is still rigid after the removal of any two connected vertices and all neighboring edges?
For the special case of the equilateral triangle, one might remove any two vertices and have an isolated vertex. I'd call that solution controversial. What is the simplest non-controversial super-bracing of a triangle? (I'll be very, very, very surprised if it's the same as the heptagon solution.)
Here's a unit diameter decagon resized by (1/φ,1,φ), with the origin added. Is it rigid? Is it super-braced?