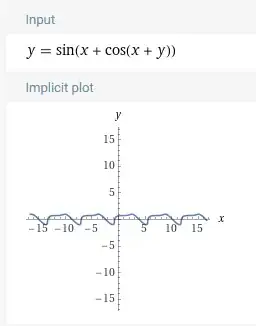
There is almost likely no closed form. However, to find the Fourier series for $y=L(x)$ in $y=\sin(x+\cos(x+y))$, substitute $y=\frac\pi2-w-x$, set $x=a$, and subtract $\sin(a)$ so the curve passes through $(\pm\pi,\pm\pi)$:
$$f(w)=\sin(\sin(w)+a)+w-\sin(a)=\frac\pi2-x-\sin(a)$$
Setting up the Fourier series for $g(x)=f^{-1}(x)$, substituting $g(t)\to t$, and integrating by parts gives:
$$g(x)=\sum_{n\in\Bbb Z}a_n e^{i nx},a_n=\frac1{2\pi}\int_{-\pi}^\pi g(t)e^{-i nt}dt=\frac in\cos(\pi n)-\frac in\int_{-\pi}^\pi e^{-inf(t)}dt$$
One extracts $a_0=\frac1{2\pi}\int_{-\pi}^\pi t df(t)=\lim\limits_{n\to0}a_n $ becoming $\sin(a)-\frac1{2\pi}\int_{-\pi}^\pi\sin(\sin(t)+a)dt=\sin(a)(1-J_0(1))$, evaluates $\sum\limits_{n\in\Bbb Z/0}\frac ine^{inx}\cos(\pi n)=x$, and takes the real part. Thereafter, a Jacobi Anger expansion is applied with the Bessel function of the first kind $J_n(x)$:
$$g(x)=\sin(a)(1-J_0(1))+x-\operatorname{Re}\sum_{n\in\Bbb Z/0}\sum_{k\in\Bbb Z}\frac{iJ_k(-n)}{2\pi n}e^{in(\sin(a)+x)} \int_{-\pi}^\pi e^{i(k(\sin(t)+a)-n t)}dt$$
The inner integral gives $J_n(x)$:
$$\boxed{f(x)=\sin(\sin(x)+a)+x-\sin(a)\implies f^{-1}(x)=\sin(a)(1-J_0(1))+x+\sum_{n\in\Bbb Z/0}\sum_{m\in\Bbb Z}\frac{(-1)^k}nJ_k(n)J_n(k)\sin(nx+n\sin(a)+ak)}$$
Since $L(x)=\frac\pi2-x-g\left(\frac\pi2-x-\sin(a)\right)$, the Fourier series is therefore:
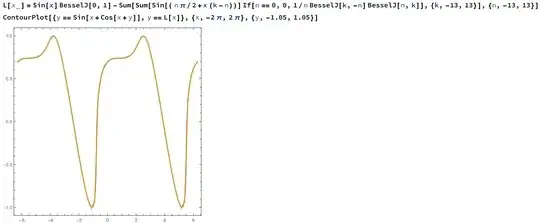
$$\bbox[2px, border: 3px blue groove]{y=\sin(x+\cos(x+y))\implies y=L(x)=\sin(x)J_0(1)-\sum_{n\in\Bbb Z/0}\sum_{m\in\Bbb Z}\frac{(-1)^k}nJ_k(n)J_n(k)\sin\left(x(k-n)+\frac{\pi n}2\right)}$$
shown here by plotting $y=L(x)$ and the truncated series:
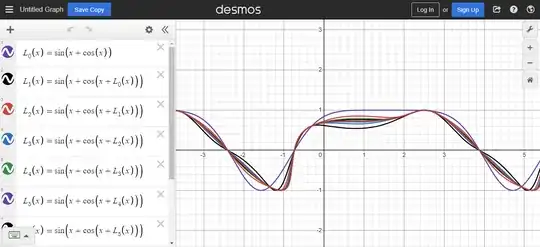 https://www.desmos.com/calculator/h2aj27gveg
https://www.desmos.com/calculator/h2aj27gveg