As titled, I want to find the inverse function of $f(x) \triangleq \ln x - x + \dfrac{1}{x}$, where $x \in (0,1]$. Note that $f(0)$ is hard to define, because $\displaystyle\lim_{x \to 0^+} f(x)\to-\infty$. We also know $f(1)=0$.
Such $f^{-1}$ exists. Because $f'(x)=\dfrac{1}{x}-1-\dfrac{1}{x^2} < 0$ when $x\in (0,1]$, thus $f$ is decreasing. However, it seems hard to find it out more explicitly.
As said in comments, you cannot solve for $x$ the equation $$y=\log(x) -x + \dfrac{1}{x}$$ but you can have the result in terms of an infinite series since $$y=-(x-1)+\sum_{n=2}^\infty (-1)^n\, \frac {n-1} n (x-1)^n$$
Using power series reversion $$x=\sum_{n=0}^\infty (-1)^n\, \frac{a_n}{n!}\,y^n$$where the first $a_n$ $$\{1,1,1,-1,-7,19,229,-1009,-17263,105211,2332141\}$$ correspond to sequence $A331404$ in $OEIS$.
According to $OEIS$ documentation, with $a_0=1$
$$a_n=\sum _{k=1}^n (-1)^{n-k}\,\binom{n}{k}\, a_{k-1} \, a_{n-k}$$
Truncating the series at $O(y^{51})$, for $y=\frac 12$ this gives $$x=\color{red}{0.6275585295}93$$
Doubling the number of terms $$x=\color{red}{0.62755852958180167}15$$
One can find a series for $g(x)=f^{-1}(x)$, with this method, but the coefficients would be recursive, not explicit. Another way is to apply the inverse Laplace transform; $g(x)’s,x>0$ Laplace transform is:
$$L_x(g(x))=\int_0^\infty e^{-st}g(t)dt=-\int_0^1 te^{-sf(t)}f’(t)dt=\frac1s-\frac1s\int_0^1 e^{-sf(t)}dt$$
after integrating by parts. Next, substitute $t\to e^t$ and apply the DLMF’s Associated Anger Weber function $A_v(z)=\frac1\pi\int_0^\infty e^{-vt-z\sinh(t)dt}$:
$$L_x(g(x))=\frac1s-\frac1s\int_0^\infty e^{(s-1)t-2s\sinh(t)}dt=\frac1s-\frac\pi sA_{s-1}(2s)$$
Taking the inverse Laplace transform gives:
$$\boxed{f(x)=\ln(x)-x+\frac1x\implies f^{-1}(x)=1-\frac1{2i}\int_{c-i\infty}^{c+i\infty}\frac{e^{sx}}sA_{1-s}(2s)ds}$$
shown here via a resource function:
First we note that the equation
\begin{equation} \log\left(x\right)-x+1/x=y \end{equation}
it comes from the equation
\begin{equation} (*)\,x-2\sinh\left(x\right)=y \end{equation}
taking the change of variable $x\rightarrow e^{x}$. We will work with this last one.
Transforming the equation with the change of variable $x\rightarrow\textrm{arccsch}\left(iz\right)$, we obtain the equation
\begin{equation} \textrm{arccsc}\left(z\right)-\frac{2}{z}-iy=0 \end{equation}
Defining the function $f(z)=\textrm{arccsch}\left(z\right)-\frac{2}{z}-iy$ and applying the Burniston-Siewert method to solve transcendental equations to this equation we obtain
\begin{equation} z=-i\left(\frac{1}{t}+m\right) \end{equation}
where
\begin{equation} m=\frac{1}{2\pi}{\displaystyle \int\limits_{0}^{1}\log\left(\frac{\left(\pi t-4\right)^{2}+4t^{2}\left(\textrm{arcsech}\left(t\right)+y\right)^{2}}{\left(\pi t-4\right)^{2}+4t^{2}\left(\textrm{arcsech}\left(t\right)-y\right)^{2}}\right)}\,dt \end{equation}
Therefore the solution to equation (*) is
\begin{equation} x=y-\frac{2}{\frac{1}{y}+m} \end{equation}
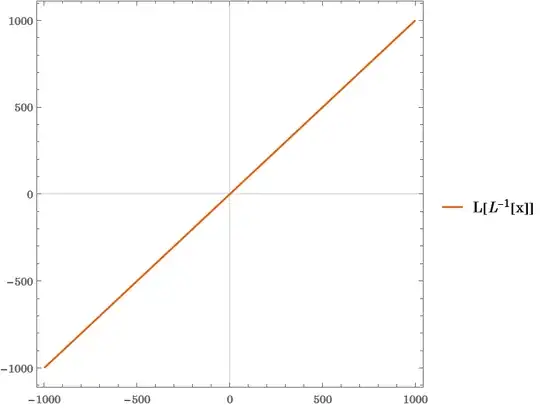
Retaking the change of variable for the original equation and placing everything in a single expression the inverse function of $L(x)=\log\left(x\right)-x+1/x$ is
\begin{equation} L^{-1}\left(x\right)=\exp\left[x-2\left[\frac{1}{x}+\frac{1}{2\pi}{\displaystyle \int\limits_{0}^{1}\log\left(\frac{\left(\pi t-4\right)^{2}+4t^{2}\left(\textrm{arcsech}\left(t\right)+x\right)^{2}}{\left(\pi t-4\right)^{2}+4t^{2}\left(\textrm{arcsech}\left(t\right)-x\right)^{2}}\right)}\,dt\right]^{-1}\right] \end{equation}
Ref:
-E. E. Burniston, C.E. Siewert. The use of Riemann problems in solving a class of transcendental equations. Mathematical Proceedings of the Cambridge Philosophical Society. 73. 111 - 118. (1973).
*-Henrici P., Applied and computational complex analysis, Volume III. Wiley, New York. 183-191 (1986).
