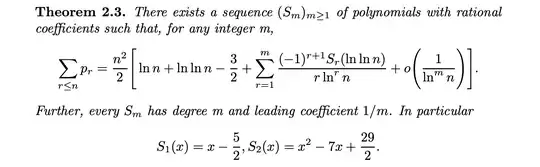The sum of the first $n$ prime numbers divided by the $(n+1)$th prime number

Question

It is known that the asymptotic behavior of the $n$th prime number is given by $$p_n\approx n\log n$$ and $$p_1+p_2+\ldots +p_n\approx {1\over 2}n^2\log n$$ These results are advanced. They imply $$ {p_1+p_2+\ldots +p_n\over p_{n+1}}\to \infty \quad (1)$$ Is there a more elementary proof of $\bf (1)$ ?

For example the condition ${p_n\over n^2}\to 0$ would be sufficient as $p_1+\ldots +p_n\ge \sum_{k=1}^nk\approx {n^2\over 2}.$

The property $(1)$ has been applied in this answer.

I was trying to use the Euler theorem $$\sum_{n=1}^\infty {1\over p_n}=\infty\quad (2)$$ in vain. The proof of property $(2)$ is not extremely hard. It makes use of basic facts concerning the infinite products.

Answer 1

Dusart proved $1998$ the bound $$ p_1+\cdots +p_n > \frac{1}{2}n^2(\log(n)+\log(\log(n))-2), $$ and $1999$ the bound $$ p_n<n(\log(n)+\log(\log(n)) $$ for all $n\ge 6$. Applying this for $p_{n+1}$ and for its reciprocal, this yields $$ \frac{p_1+\cdots +p_n}{p_{n+1}}>\frac{n^2}{4(n+1),} $$ which tends to infinity for $n\to \infty$. Dusart's proof is fairly elementary, but there might be still an easier bound.

Reference:

Asymptotic expression for sum of first n prime numbers?

Answer 2

Starting form the Prime number Theorem (which has an elementary proof due to Erdos and Selberg), an elementary derivation of an asymptotic formula for the sum of the first $n$ primes can be found in Theorem 2.3 of this paper. This result proves that

Alternatively, since $p_n \sim n\log n < n^{1+\epsilon}$ for any $\epsilon > 0$, as $n \to \infty$ it implies the proportion of numbers formed by the sequence of ratios $\frac{p_1}{p_n},\frac{p_2}{p_n} \ldots, \frac{p_{n}}{p_n}$ which fall inside any sub-interval within $(0,1)$ is proportion to the length of that interval i.e. the sequence $\frac{p_r}{p_n}$ approaches equidistribution in $(0,1)$ as $n \to \infty$. Hence we have

Theorem: Let $p_k$ be the $k$-th prime and let $f$ be a continuous function Riemann integrable in $(0,1)$ then, $$ \lim_{n \to \infty}\frac{1}{n}\sum_{r = 1}^{n}f\Big(\frac{p_r}{p_n}\Big) = \int_{0}^{1}f(x)dx. $$

(See the proof of the theorem in this MO link). Taking $f(x) = x$, we get

$$ p_1 + p_2 + \cdots + p_n \approx \frac{n p_n}{2} \approx \frac{n^2 \log n}{2} \approx \frac{n p_{n+1}}{2} $$ since by the Prime number Theorem, $\displaystyle \frac{p_{n+1}}{p_n} \to 1$.