Compute $\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{1}{e^x+e^{-x}+1}\ dx$

Question

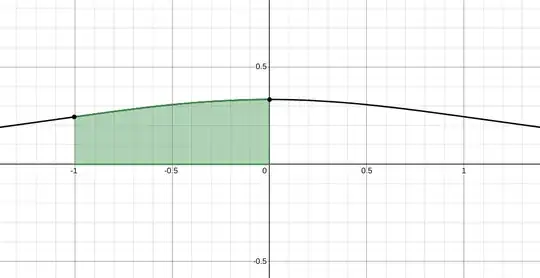
Let's consider

$$\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{1}{e^x+e^{-x}+1}\ dx$$

First, I note that

$$\frac{1}{e^x+e^{-x}+1}=\frac{1}{e^{-x}(e^{2x}+e^{x}+1)}=\frac{e^x}{e^{2x}+e^x+1}$$

So, I can rewrite the integral as follows:

$$\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{1}{e^x+e^{-x}+1}\ dx=\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{e^x}{e^{2x}+e^{x}+1}\ dx$$

I use the following substitution:

$$t=e^x \Longrightarrow dt=e^x dx$$

and then

$$\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{e^x}{e^{2x}+e^{x}+1}\ dx=\int_{1}^{\frac{\sqrt{3}-1}{2}} \frac{1}{t^2+t+1}\ dt=\int_{1}^{\frac{\sqrt{3}-1}{2}} \frac{1}{\left(t+\frac{1}{2}\right)^2+\frac{3}{4}}\ dt=$$

$$=\frac{4}{3}\int_{1}^{\frac{\sqrt{3}-1}{2}} \frac{1}{\left(\frac{2t+1}{\sqrt{3}}\right)^2+1}\ dt=\frac{2}{\sqrt{3}}\left[\arctan\left(\frac{2t+1}{\sqrt{3}}\right)\right]^{\frac{\sqrt{3}-1}{2}}_1=\frac{2}{\sqrt{3}}\left(\frac{\pi}{4}-\frac{\pi}{6}\right)=\frac{\pi}{6\sqrt{3}}$$

But, observing that $\frac{\sqrt{3}-1}{2}<1$, I have to put a minus sign to the result, therefore, I get:

$$\int_{0}^{\ln\left(\frac{\sqrt{3}-1}{2}\right)} \frac{1}{e^x+e^{-x}+1}\ dx=-\frac{\pi}{6\sqrt{3}}$$

Is it correct? Is there a faster way to solve it?

Answer 1

Note that the substitution $e^x= \frac{1-\sqrt3 t}{1+\sqrt3t}$ simplifies the integral

$$\int_{0}^{\ln\frac{\sqrt{3}-1}{2}} \frac{1}{e^x+e^{-x}+1}dx =-\frac2{\sqrt3}\int_0^{\tan \frac\pi{12}}\frac1{1+t^2}dt=-\frac{\pi}{6\sqrt3} $$

Answer 2

You can't just "put a minus sign". It's good that you recognize that $a = \frac{\sqrt{3}-1}{2} < 1$, and its consquence: the upper limit is less than the lower limit and since $f(x) = \bigl(e^{x}+1+e^{-x}\bigr)^{-1}$ is positive, the value of the definite integral must be negative. Note: $\ln a \approx -1.005$, so it looks like $-1$ but it's not quite!

But, you've made a mistake: $\arctan(\sqrt{3}\,) = \tfrac{\pi}{3}$, so the value of the integral is $$ \frac{2}{\sqrt{3}} \biggl( \frac{\pi}{4} - \frac{\pi}{3} \biggr) = - \frac{\pi}{6\sqrt{3}} = - \frac{\pi\sqrt{3}}{18} \approx -0.3023 $$

By a happy (unhappy?) coincidence, $$ \frac{\pi}{4} - \frac{\pi}{3} = -\frac{\pi}{12} $$ and $$ \frac{\pi}{4} - \frac{\pi}{6} = \frac{\pi}{12}, $$ which is why your (incorrect) answer was only off by a sign.

Answer 3

Your answer is correct, but you have made $2$ mistakes in the last few steps:

$$=\frac43\int_1^\frac{\sqrt3-1}2\frac1{\left(\frac{2t+1}{\sqrt3}\right)^2+1}dt=\frac2{\sqrt3}\left[\arctan\left(\frac{2t+1}{\sqrt3}\right)\right]^{\frac{\sqrt3-1}2}_1=\frac2{\sqrt3}\left(\frac\pi4-\color{red}{\frac\pi6}\right)=\frac\pi{6\sqrt3}$$ But, observing that $\color{red}{\text{$\frac{\sqrt3-1}2<1$, I have to put a minus sign to the result}}$, therefore, I get: $$\int_0^{\ln\left(\frac{\sqrt3-1}2\right)}\frac1{e^x+e^{-x}+1}dx=-\frac\pi{6\sqrt3}$$

Note that $\tan^{-1}\sqrt3=\frac\pi3$ and you have to plug in the values of $t$ from the limits in the same order as they are written. This is the statement of the $2^\text{nd}$ part of the FTC):

$$\int_a^bf'(x)\mathrm dx=f(b)-f(a)$$

Now, rewriting the given integral as $$\begin{align}\mathcal I&=\int_0^{\ln\left(\frac{\sqrt3-1}2\right)} \frac{\mathrm dx}{e^x+e^{-x}+1}\\&=\int_0^{\ln\left(\frac{\sqrt3-1}2\right)} \frac{\mathbb dx}{2\cosh x+1}\end{align}$$

$\textbf{Alternative method 1:}$ By the tangent half-angle substitution:

$$t=\tanh\left(\frac{x}2\right)\implies\mathrm dx=\frac{2\mathrm dt}{1-t^2},\cosh x=\frac{1+t^2}{1-t^2}$$ $$\begin{align}\implies\mathcal I&=2\int_0^{\frac{\sqrt3-3}{\sqrt3+1}}\frac{\mathrm dt}{3+t^2}\\&=\frac2{\sqrt3}\left[\tan^{-1}\left(\frac{x}{\sqrt3}\right)\right]_0^{\frac{\sqrt3-3}{\sqrt3+1}}\\&=-\frac2{\sqrt3}\tan^{-1}\left(\frac{\sqrt3-1}{\sqrt3+1}\right)\\&=\boxed{-\frac{\pi}{6\sqrt3}}\end{align}$$

$\textbf{Alternative method 2:}$ Substitute $2\cosh x+1=\frac1v$:

$$\begin{align}\mathcal I&=-\int_\frac13^\frac{\sqrt3-1}3\frac{\mathrm dv}{\sqrt{-3v^2-2v+1}}\\&=-\frac1{\sqrt3}\sin^{-1}\left(\frac{3v+1}2\right)\Bigg|_\frac13^\frac{\sqrt3-1}2\\&=\frac{\frac\pi3-\frac\pi2}{\sqrt3}\\&=\boxed{-\frac\pi{6\sqrt3}}\end{align}$$

Answer 4

Here is another way to solve the integral that involves hyperbolic functions. Recall that $\cosh(x)=\frac{e^x+e^{-x}}{2}$

Immediately we see: $$\int\frac{dx}{e^x+e^{-x}+1}=\int\frac{dx}{2\cosh(x)+1}$$ Using the substitution $u=\frac{\tanh(\frac x2)}{\sqrt3}$ we're left with the integrand $\frac{1}{u^2+1}$ which of course is $\arctan(u)$. Remember to change the bounds, and after computing we get $-\frac{\pi}{6\sqrt3}$

Answer 5

(Yes, I later found another answer saying the same thing. But I think it good to tell the OP twice lest (s)he miss it.)

You made a slight error. I highlight where the problem is with red coloration:

$$=\frac{4}{3}\int_{1}^{\frac{\sqrt{3}-1}{2}} \frac{1}{\left(\frac{2t+1}{\sqrt{3}}\right)^2+1}\ dt=\frac{2}{\sqrt{3}}\left[\arctan\left(\frac{2t+1}{\sqrt{3}}\right)\right]^{\frac{\sqrt{3}-1}{2}}_1\color{red}{=\frac{2}{\sqrt{3}}\left(\frac{\pi}{4}-\frac{\pi}{6}\right)}=\frac{\pi}{6\sqrt{3}}$$

When you substituted values for $t$, you got $(2/\sqrt3)\arctan(1)$ at the upper boundary and $(2/\sqrt3)\arctan(\sqrt3)$ at the lower boundary, then apparently rendered $\arctan(1)=\pi/4$ and $\arctan(3/\sqrt3)=\arctan(\sqrt3)=\pi/6$. But, in fact, $\arctan(\sqrt3)=\pi/3$. With the proper substitution of values, you get the negative sign without having to "fudge" it in:

$$=\frac{4}{3}\int_{1}^{\frac{\sqrt{3}-1}{2}} \frac{1}{\left(\frac{2t+1}{\sqrt{3}}\right)^2+1}\ dt=\frac{2}{\sqrt{3}}\left[\arctan\left(\frac{2t+1}{\sqrt{3}}\right)\right]^{\frac{\sqrt{3}-1}{2}}_1\color{blue}{=\frac{2}{\sqrt{3}}\left(\frac{\pi}{4}-\frac{\pi}{3}\right)}=-\frac{\pi}{6\sqrt{3}}$$