Solving a second order separable differential equation but having problems integrating $\ln(1-x)$ because $\ln(0)$ is not defined

Question

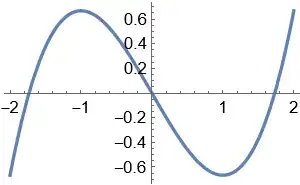
Problem:

Solve the following differential equation: $$ \frac{ d^2 s }{dt^2} = g(1 -s^2) $$ with the following initial condition: \begin{align*} \dfrac{ ds}{dt} \left( 0 \right) &= 0 \\ s(0) &= \dfrac{1}{4} \\ \end{align*} and $g$ is a positive constant.

Note: This differential equation is from a physics problem I am working on.

Answer:

\begin{align*} \frac{ d^2 s }{dt^2} &= g(1 -s^2) \\ \frac{ d^2 s} {dt^2} + gs^2 &= g \\ \frac{ d^2 s} {dt^2} &= g - gs^2 \\ d^2s &= g (1- s^2) \,\, dt^2 \\ \dfrac{ d^2 s}{1-s^2} &= g \,\, dt^2 \\ \end{align*} Now we integrate both sides. To integrate the left side, we apply the technique of partial fractions. \begin{align*} \dfrac{ 1}{1-s^2} &= \dfrac{A}{1-s} + \dfrac{B}{1+s} \\ 1 &= A(1+s) + B(1-s) \\ A + B &= 1 \\ A - B &= 0 \\ A &= B \\ A &= \dfrac{1}{2} \\ B &= \dfrac{1}{2} \\ \end{align*} Hence we have: $$ \int \dfrac{ 1 }{1-s^2} \,\, ds = \dfrac{1}{2} \ln{|1-s|} + \dfrac{1}{2} \ln{|1+s|} + C_1 $$ Going back to the differential equation we have: \begin{align*} \left( \dfrac{1}{2} \ln{|1-s|} + \dfrac{1}{2} \ln{|1+s|} \right) \,\, ds &= gt \,\, dt + C \\ % \dfrac{ds}{dt} &= \dfrac{ gt }{ \dfrac{1}{2} \ln{|1-s|} + \dfrac{1}{2} \ln{|1+s| } } + C \\ \end{align*} We know that $\dfrac{ ds }{dt}\left( 0 \right) = 0$. We also know that when $t = 0$ that $s = 1/4$. Hence we eliminate the constant. \begin{align*} 0 &= \dfrac{ g(0) }{ \dfrac{1}{2} \ln{|1-\dfrac{1}{4}|} + \dfrac{1}{2} \ln{|1+\dfrac{1}{4}| } } + C \\ 0 &= 0 + C \\ C &= 0 \\ \dfrac{ds}{dt} &= \dfrac{ gt }{ \dfrac{1}{2} \ln{|1-s|} + \dfrac{1}{2} \ln{|1+s| } } \\ \end{align*} Now we have the following first order differential equation. $$ \ln{|1-s|} + \ln{| 1+s | } \,\,\, ds = 2gt \,\, dt $$ Now we need to integrate both sides. However, there is a problem when $s = 1$ because $\ln{0}$ is not defined. What did I do wrong?

Answer 1

From my comment, $$u \ du =g(1-s^2)ds\\\implies \frac{u^2}{2}=gs-g\frac{s^3}{3}+C_0\\\implies u=\frac{1}{\sqrt3}\sqrt{6gs-2gs^3+C_1}$$ According to given data, $$0=\frac{6g}{4}-\frac{g}{32}+C_1\implies \frac{C_1}{g}=\frac{-47}{32}$$ So $$\frac{ds}{\sqrt{6gs-2gs^3-\frac{47g}{32}}}=\frac{dt}{\sqrt 3}$$ Hope you'll be able to continue from here, although I can't find any methods to solve the indefinite integral

Answer 2

Too long for a comment.

I think that your process is not correct since you worked with $\frac{d^2s}{dt^2}$ as you would do with $\frac{ds}{dt}$.

This looks to be a monster since, without any boundary condition, the solution is given in terms of the Weierstrass elliptic function.

What Mathematica returns is $$s(t)=k\, \wp\left(\frac{t+c_1}{k};\frac{12}{k^2},c_2\right) \quad \text{where} \quad k=\sqrt[3]{-\frac 6g }$$ Applying the conditions would lead to two hideous equations $$k \,\wp\left(\frac{c_1}{k};\frac{12}{k^2},c_2\right)=\frac 14 \qquad \text{and} \qquad \wp'\left(\frac{c_1}{k};\frac{12}{k^2},c_2\right)=0$$

What you could do is to switch variables and try to solve $$\frac {t''}{[t']^3}+g(1-s^2)=0$$ Using $p=t'$ $$p=\pm \sqrt{\frac{3}{2 g s \left(3-s^2\right)+c_1} }$$

Integrating again leads to very complex elliptic integrals and no way to inverse it excpet again in terms of a Weierstrass elliptic function !

Answer 3

I use Mathematica for controlling parameters in a transparent way.

Multiplying both sides by $\frac{ds}{dt}$ and solving for $dt^2$ yields the standard elliptic integral, the inverse of the Jacobi amplitude

$$\frac{\left(s'\right)^2}{2}=g \left(s-\frac{s^3}{3}\right)\ + \ g \ U$$

g dt^2 /. 
    Solve[1/2 (ds/dt)^2 +  s g  ( 1/3 s^2 - 1) == g U, dt][[-1]] // Simplify

$$g \ \text{dt}^2 = \frac{3}{2} \ \frac{3 \text{ds}^2}{3 U +3 s-s^3}$$ Orbit forms depend on the value of the total energy U.

The potential $$V(s)= g \ (\frac{s^3}{3}-s)$$ has two extrema.

So there are three classes of orbits

1. High energy $U \gt \frac{2}{3}$, impact from left, repulsion somrwhere at $ s>0$ for $s'=0$
2. energy less maximum, the same but repulsion left of the maximum
3. energy between local minimum and maximum, oscillation inside the pot

Fortunately all the algebra of elliptic integrals and its inverses operates on the field of elliptic functions, analytic in both variables. So one may rely on the quadratic forms of the integrals and their inverses and do root analysis after deriving the standard form.

In Mathematica a 1-liner. We solve for the squares of $t$ and the square of the elliptic integral as a function of $s$, rename the three roots by $r_n$ and replace the cubic by the root product.

 Solve[g (t-Subscript[t, 0])^2 == 
    ((Sqrt[3/2] (\[Integral]1/Sqrt[3 U +3 s- s^3] \[DifferentialD]s))^2//. 
      {Root[_,n_Integer]:>Subscript[r, n]}//Simplify )/.
      {a__*(-3 s+s^3-3 U)^k_:>
       a* ((s-Subscript[r, 1])(s-Subscript[r, 2])(s-Subscript[r, 3]))^k},s][[-1]]//
  PowerExpand

$$\left.s\to r_2 \text{sn}\left(\frac{i \sqrt{g} \sqrt{r_1-r_3} \left(t-t_0\right)}{\sqrt{6}}|\frac{r_2-r_3}{r_1-r_3}\right){}^2-r_3 \text{sn}\left(\frac{i \sqrt{g} \sqrt{r_1-r_3} \left(t-t_0\right)}{\sqrt{6}}|\frac{r_2-r_3}{r_1-r_3}\right){}^2+r_3\right\}$$

The imaginary $i$ can be hided in the square roots. Further discussion needs energy vulues, reduction of the modulus to values in (0,1) and the start point $s_0$.

As a general fact, the Jacobi amplitude, the inverse of th elliptic intergral $F(\phi|k)$ is quasi periodic for real modulus in $k\in(0,1)$ decribing rotations, such that $\text{sn}(x|k)= \sin \text{am}(x|k)$ and $\text{cn}(x|k)= \cos \text{am}(x,k)$ are peridic on the full circle.

For modulus $k>1$ the $\text{am}(x|k)$ function with derivative $\text{dn}(x,k)$ becomes the antiderivative of a scaled $\text{cn}$ function, i.e. a periodic function describing oscillation on a part of the full circle only.

Special advice for users of Mathematica and Abraham/Stegun tables: their modulus is $m=k^2$, obscuring the analytic feature in both variables, but makes it easier to identify its pattern in fomulas involving $k^2$.

Answer 4

Maple also helps with initial condition $s(0)=s_0$:

$$s(t)=-\frac{6}{g}\cdot \wp \left(t+\tau, \frac{g^2}{3}, -\frac{g^{3} s_{0} \left(s_{0}^{2}-3\right)}{54} \right)$$

with $\tau=\mathit{RootOf}\left(s_{0}\cdot g+6\cdot \wp\! \left(\tau,\frac{g^{2}}{3},-\frac{g^{3} s_{0} \left(s_{0}^{2}-3\right)}{54}\right)=0, \tau\right)$

Example for $s_0=\frac{1}{4}, g=1$:

Solution for $\tau$: $$\{\tau \to \fbox{$(2.3403\, +2.58906 i)+4.6806 c_1+(0.\, +5.17813 i) c_2\text{ if }(c_1|c_2)\in \mathbb{Z}$}\}$$

Any $\tau$ value may be chosen.

Plot $s(t), g=1$:

Hint: $\wp(z,g_2,g_3)$ is the Weierstrass P function