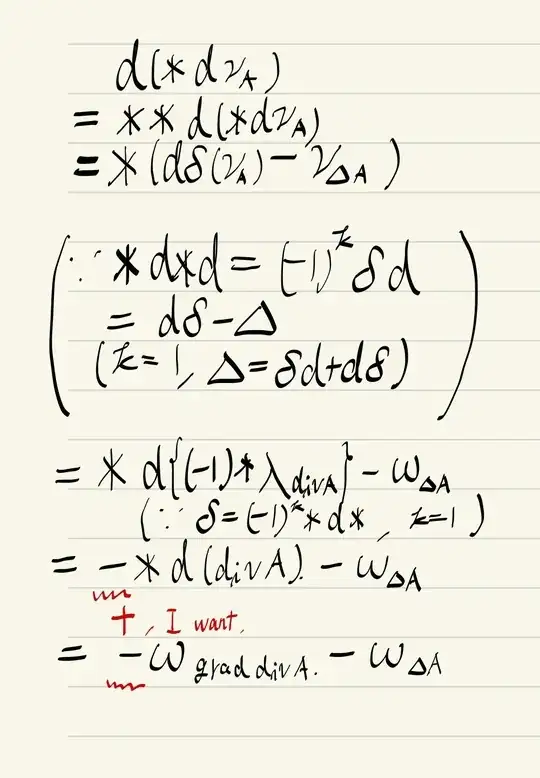$ \operatorname{rot}(\operatorname{rot} A)$ by differential form

Question

I am curious whether it's possible to prove $ \operatorname{rot}(\operatorname{rot} A) $ using differential forms, similar to the example shown below. I believe the Hodge star operator might play a role in this, but I would appreciate an explanation if anyone is familiar with this approach.

Example of a proof using differential forms:

$$ \mathrm{div}(fa) = (\nabla f) \cdot a + f (\nabla \cdot a) $$

Let $ \lambda_v $ be a 3-form and $ \omega_v $ a 2-form, both with components corresponding to the vector $ v $.

$$ \lambda_{\mathrm{div}(fa)} = d(f\omega_a) = df \wedge \omega_a + f(d\omega_a) \quad (\text{by the product rule}) \\ = \lambda_{\mathrm{grad} f \cdot a} + \lambda_{f\mathrm{div}(a)} \\ = \lambda_{\mathrm{grad} f \cdot a + f\mathrm{div}(a)} $$

Regarding the proof of $ \operatorname{rot}(\operatorname{rot} A) $:

I think there might be a way to prove it using the following expression:

$$ \omega_{\operatorname{rot}(\operatorname{rot} A)} = d(*d\nu_A) = ? $$

Here, $ \nu_A $ is a 1-form whose components correspond to those of $ A $. I suspect the properties of the Hodge star operator could be useful here. While I could verify this calculation component-wise without using differential forms, I am searching for a more efficient, conceptual method that fully leverages the power of differential forms, similar to the approach used in the example above.

I have also considered using the Laplace-de Rham operator, but when I worked through the calculation, I encountered sign issues and didn't obtain the desired result(like the picture below). I am not entirely confident in my reasoning and would appreciate any insights. If anyone could provide a clear proof or point out where my calculation may have gone wrong, that would be extremely helpful.

Answer 1

Its a very simple map: Any vector field euclidean $\mathbb R^3$can be transformed to a 1-component field by

$$\sum_i A_i(x) \ dx^i = \tilde A_1(y) dy^1$$ with exterior derivative $$d \tilde A_1(y) dy^1 = \partial_2\ \tilde A_1(y) \ dy^2\wedge dy^1 \ + \ \partial_3\ \tilde A_1(y) \ dy^3\wedge dy^1 $$ It's Hodge dual is the scalar product wirth the volume form $$\star (d \tilde A_1(y) dy^1 ) \ = \ \partial_2 \tilde A_1(y)\ \langle dy^2\wedge dy^1 , \ \ dy^1\wedge dy^2\wedge dy^3 \rangle + \partial_3 \tilde A_1(y) \ \langle dy^3\wedge dy^1, \ \ dy^1\wedge dy^2\wedge dy^3 \rangle = \ \partial_2 \tilde A_1(y)\ dy ^3 \ - \ \partial_3 \tilde A_1(y) \ dy ^2$$
Generalize by adding the circular terms $1\to 2\to 3\to 1.$

Finally

$$d \star d \tilde A_1(x) \ dy^1 \ = \ \partial_{1,2} \tilde A_1(y)\ dy^1\wedge dy^3 + \partial_{2,2} \tilde A_1(y)\ dy^2\wedge dy^3 - \ \partial_{3,1} \tilde A_1(y) \ dy^1\wedge dy^2 - \ \partial_{3,3} \tilde A_1(y) \ dy^3\wedge dy ^2$$

Going back to 1-forms

$$\begin{align}&\star d \star d \tilde A_1(x) \ dy^1 \ \\&= \langle(- \partial_{1,2} \tilde A_1(y)\ dy^3 + \ \partial_{1,3} \tilde A_1(y) \ dy^2) \wedge dy^1 + ( \partial_{2,2} \tilde A_1(y)\ \ + \ \partial_{3,3} \tilde A_1(y) ) \ dy^2\wedge dy ^3, \quad dy^1\wedge \ dy^2 \wedge dy^3\rangle \\ & (\partial_{i,i} A_k - \partial_{ik} A_i)dx^k \end{align}$$

This complies to

$$\nabla \times(\nabla \times \ A) = \nabla (\nabla \cdot A) - (\nabla \cdot \nabla) A $$ up to a sign. The difference is $$\star^2 A =-A$$

Answer 2

The so called BAC-CAB formula $$\tag1 \nabla\times(\nabla\times A)=\nabla(\nabla\cdot A)-\Delta A $$ is well known and it is interesting to try to write it in terms of differential forms.

I claim this leads to $$\tag2 \star\,d\,\star dA^\flat=d\,\star d\,\star A^\flat\color{red}{+}(d\delta+\delta d)A^\flat $$ where $$\tag3 \delta=(-1)^k\star\,d\,\star $$ is the codifferential and $k$ is the grade of the form it acts on.

That the LHS and the first terms of the RHS of (1) and (2) agree is easy to see.

The rest of this post will mostly try to explain the $\color{red}{red}$ plus sign in (2).

I stress that we are working in $\mathbb R^3$ with Euclidean signature. Then the Hodge dual is, as we know, defined by $$\tag4 \star\,dx=dy\wedge dz,\quad\star\,dy=dz\wedge dx,\quad\star\,dz=dx\wedge dy\,,\quad \star(dx\wedge dy\wedge dz)=1 $$ and $$\tag5 \star\,\star=1\,. $$ To see that the Hodge-Laplace-de Rham operator $d\delta+\delta d$ is the classical Laplace operator when it acts on $0$-forms (functions) observe that

\begin{align} &k=0\,,&(d\delta+\delta d)f&=d\star \underbrace{d\,\star f}_{0}+\star\, d\star df=\star\,d\big(f_{,x}\,dy\wedge dz+f_{,y}\,dz\wedge dx+f_{,z}\,dx\wedge dy\big)\\ &&&=\Delta f\,\tag6 \end{align} where the subscript $,x$ means partial differentiation w.r.t. $x$ and so on.

However, in (2) the form $A^\flat$ is the $1$-form $$\tag7 A_x\,dx+A_y\,dy+A_z\,dz $$ and $dA^\flat$ is a $2$-form. By (3) this leads to \begin{align}\tag8 &k=1,2\,,&(d\delta+\delta d)A^\flat&=\color{red}{-}d\star d\,\star \underbrace{A^\flat}_{\text{$1$-form}}\color{red}{+}\star\, d\star\underbrace{ dA^\flat}_{\text{$2$-form}} \end{align} which proves (2).