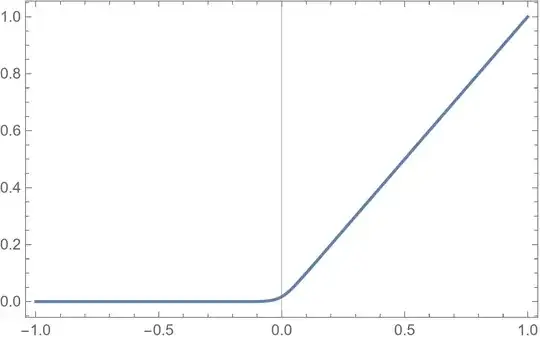
Your function $f(x,a,b,L) = L + \max(b(x-a),0)$ can be obtained from the basic "ramp" function $R(x) = \max(x,0)$ via shifting and rescaling:
\begin{equation}
f(x,a,b,L) = L + R(b(x-a))
\end{equation}
Therefore it suffices to find a smooth approximation to $R(x)$, from which $f(x,a,b,L)$ can be obtained for any values of $a$, $b$, and $L$. $R(x)$ can be written as the integral of the Heaviside step function
\begin{equation}
H(x) =
\begin{cases}
1 & x > 0\\
0 & x < 0
\end{cases}
\end{equation}
(For the purposes of this answer, the value of $H(0)$ doesn't matter.) That is:
\begin{equation}
R(x) = \int_{-\infty}^x H(y)\, dy \qquad\qquad (1)
\end{equation}
Now, a useful approximation to $H(x)$ is
\begin{equation}
H(x) \approx \frac{1}{2}\left(1 + \tanh\left(\frac{x}{\epsilon}\right)\right)\, ,\qquad\qquad (2)
\end{equation}
where $\epsilon$ is some small positive number. Plugging this approximation into Eq. (1) yields:
\begin{equation}
R(x) \approx \int_{-\infty}^x \frac{1}{2}\left(1 + \tanh\left(\frac{y}{\epsilon}\right)\right)\, dy
\;=\;
\frac{1}{2}\left(x + \epsilon\log\left(2\cosh\left(\frac{x}{\epsilon}\right)\right)\right)\qquad (3)
\end{equation}
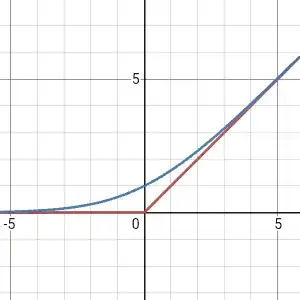
For gradient-based algorithms, this approximation of $R(x)$ has the advantage that its derivative is given simply by Eq. (2). Eq. (3) is plotted below for $\epsilon = 0.05$.