2

I am trying to show that

$$\int_0^{\infty} \frac{\log(x)^2}{1+x^2}dx = \pi^3/8$$

by integrating over a certain contour, but am having some trouble. I first holomorphically extend $\log$ to the region $\{ z \in \mathbb C: z \neq ix \operatorname{ for some } x \leq 0\}$ by setting

$$\log(re^{i \theta}) = \ln r + i \theta : - \frac{\pi}{2} < \theta < \frac{3 \pi}{2}\}$$

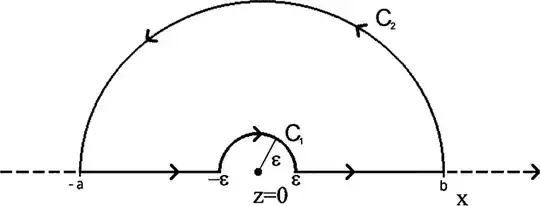
and then I integrate $\log(z)^2/(1+z^2)$ over the region

enter image description here

letting $\epsilon$ go to $0$ and $a, b$ go to $\infty$. The only singularity of $\log(z)^2/(1+z^2) = \log(z)^2/\Big((z+i)(z-i)\Big)$ inside this region is at $z = i$, for which the residue is

$$\frac{\log(i)^2}{2i} = \frac{(\pi i/2)^2}{2i} = -\frac{\pi^2}{8i}$$

Assuming the circular paths go to $0$ (which I haven't proven yet), the residue theorem then implies that

$$2 \int\limits_0^{\infty} \frac{\log(x)^2}{1+x^2} dx = 2 \pi i \Big(- \frac{\pi^2}{8i}\Big) = - \frac{\pi^3}{4}$$

or

$$\int_0^{\infty} \frac{\log(x)^2}{1+x^2} dx = - \frac{\pi^3}{8}.$$

I don't know why this minus sign appeared. Where am I going wrong?

Lucenaposition
  • 2,416
D_S
  • 35,843

1 Answers1

1

Your mistake seems to be that you are assuming that the integral over the negative part of the x-axis is the same as over the positive part. This is not true. When $x$ is negative, the choice of logarithm satisfies $\log(x) = i\pi + \ln(-x)$. For such $x$, you have

$$\frac{\log(x)^2}{1+x^2} = \frac{(i \pi + \ln(-x))^2}{1+x^2} = \frac{-\pi^2 + 2 \pi i \ln(-x) + \ln(-x)^2}{1+x^2} $$ and therefore

$$\int_{-\infty}^{0} \frac{\log(x)^2}{1+x^2}dx =\int_{-\infty}^{0} \frac{-\pi^2}{1+x^2}dx + \int_{-\infty}^{0} \frac{2 \pi i \ln(-x)}{1+x^2}dx + \int_{-\infty}^{0} \frac{\ln(-x)^2}{1+x^2}dx.$$

Let's evaluate each of these integrals. The first integral is

$$\int_{-\infty}^{0} \frac{-\pi^2}{1+x^2}dx = - \pi^2 \arctan(x) \Bigg|_{-\infty}^0 = -\frac{\pi^3}{2}.$$

The second integral actually comes out to zero, because

$$\int_{-\infty}^{0} \frac{\ln(-x)}{1+x^2}dx = \int_0^{\infty} \frac{\ln(x)}{1+x^2}dx = \int_0^{1} \frac{\ln(x)}{1+x^2}dx + \int_1^{\infty} \frac{\ln(x)}{1+x^2}dx$$

and setting $u = x^{-1}$, we have $dx = -u^{-2}du$, so

$$\int_1^{\infty} \frac{\ln(x)}{1+x^2}dx = \int_1^0 \frac{\ln(u^{-1})}{1+u^{-2}} \frac{-du}{u^2} = - \int_0^1 \frac{\ln(u)}{1+u^2} du = - \int_0^1 \frac{\ln(x)}{1+x^2} dx.$$

The third integral is

$$\int_{-\infty}^{0} \frac{\ln(-x)^2}{1+x^2}dx = \int_{0}^{\infty} \frac{\ln(x)^2}{1+x^2}dx.$$

Putting all this together with the residue theorem and the fact that the semicircle contours go to zero, we have

$$-\frac{\pi^3}{2} + 2 \int_{0}^{\infty} \frac{\ln(x)^2}{1+x^2}dx = - \frac{\pi^3}{4}$$

which gets you the correct answer.

D_S
  • 35,843