Define
$$ I = \int_{-\infty}^{\infty} f(x) \, \mathrm{d}x, \qquad f(z) = \frac{1 - e^{i\pi z^2}}{(e^{\pi z} - e^{-\pi z})^2}. $$
This is related to OP's integral via the following computation:
\begin{align*}
\int_{0}^{\infty} \frac{\sin(\pi x)}{e^{2\pi\sqrt{x}} - 1} \, \mathrm{d}x
&= \int_{0}^{\infty} \frac{2x \sin(\pi x^2)}{e^{2\pi x} - 1} \, \mathrm{d}x \\
&= \left[ \frac{1 - \cos(\pi x^2)}{\pi (e^{2\pi x} - 1)} \right]_{0}^{\infty} + 2 \int_{0}^{\infty} \frac{e^{2\pi x}(1 - \cos(\pi x^2))}{(e^{2\pi x} - 1)^2} \, \mathrm{d}x \\
&= \operatorname{Re}(I).
\end{align*}
By noting that $f(z)$ is meromorphic with poles $\pm i, \pm 2i, \ldots$ and using some estimates, it is not hard to show that for any sufficiently small $\varepsilon > 0$, we can shift the contour of integration of $I$ (red line) to the blue contour as follows:
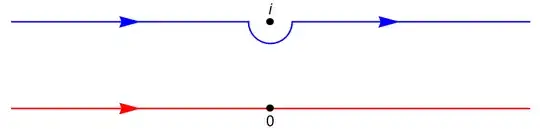
This shift of contour leads
$$ I = I_1 + I_2, $$
where
\begin{align*}
I_1 = \int_{\text{circular arc}} f(z) \, \mathrm{d}z
\qquad\text{and}\qquad
I_2 = \int_{\text{rays}} f(z) \, \mathrm{d}z.
\end{align*}
Now by expanding $f(z)$ about $z = i$, we get
$$ f(z) = \frac{1}{2\pi^2 (z-i)^2} - \frac{1}{2\pi (z-i)} + \mathcal{O}(1), $$
and this immediately yields the asymptotic expansion
\begin{align*}
I_1
&= \int_{-\pi}^{0} f(i + \varepsilon e^{i\theta}) (\varepsilon i e^{i\theta}) \, \mathrm{d}\theta \\
&= -\frac{1}{\pi^2 \varepsilon} - \frac{i}{2} + \mathcal{O}(\varepsilon).
\end{align*}
On the other hand, noting that $e^{i\pi(x+i)^2} = -e^{i\pi x^2}e^{-2\pi x}$, we get
\begin{align*}
I_2
&= \int_{\varepsilon}^{\infty} [f(i+x) + f(i-x)] \, \mathrm{d}x \\
&= \int_{\varepsilon}^{\infty} \frac{2 + e^{i\pi x^2}(e^{2\pi x} + e^{-2\pi x})}{(e^{\pi x} - e^{-\pi x})^2} \, \mathrm{d}x \\
&= \int_{\varepsilon}^{\infty} \frac{4}{(e^{\pi x} - e^{-\pi x})^2} \, \mathrm{d}x
- 2 \int_{\varepsilon}^{\infty} \frac{1 - e^{i\pi x^2}}{(e^{\pi x} - e^{-\pi x})^2} \, \mathrm{d}x
+ \int_{\varepsilon}^{\infty} e^{i\pi x^2} \, \mathrm{d}x \\
&= \frac{2}{\pi(e^{2\pi \varepsilon} - 1)}
- I
+ \int_{0}^{\infty} e^{i\pi x^2} \, \mathrm{d}x
+ \mathcal{O}(\varepsilon).
\end{align*}
Combining altogether and simplifying, it follows that
\begin{align*}
I
&= \frac{1}{\pi(e^{2\pi \varepsilon} - 1)} - \frac{1}{2\pi^2 \varepsilon}
- \frac{i}{4}
+ \frac{1}{2}\int_{0}^{\infty} e^{i\pi x^2} \, \mathrm{d}x
+ \mathcal{O}(\varepsilon) \\
&= -\frac{1}{2\pi} - \frac{i}{4} + \frac{1 + i}{4\sqrt{2}} + \mathcal{O}(\varepsilon).
\end{align*}
Since the left-hand side is independent of $\varepsilon$, letting $\varepsilon \to 0^+$ and taking real parts only yields
$$ \operatorname{Re}(I) = \frac{1}{4\sqrt{2}} - \frac{1}{2\pi}, $$
confirming @JJacquelin's conjecture.
