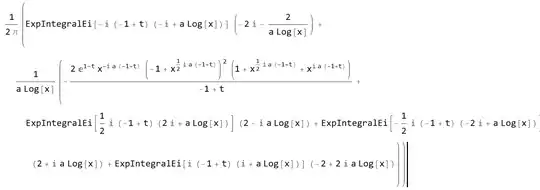computing $\frac{1}{2\pi i}\int\limits_{(1)}\frac{e^{(1-t)s}}{s}\Psi\left(\frac{\Im (s)}{\log x}\right)ds$

Question

I was reading this and got stuck right before Remark $1$. Let $$F(t)=\frac{1}{2\pi i}\int\limits_{(1)}\frac{e^{(1-t)s}}{s}\Psi\left(\frac{\Im (s)}{\log x}\right)ds$$ where $\Psi$ is a smooth cut off function zero outside of $[-\epsilon,\epsilon]$ and one inside $[-\epsilon/2,\epsilon/2]$ and where $(1)$ is the line with $\Re(s)=1$. So $F(t)$ is kinda a "cut off" version of $$\frac{1}{2\pi i}\int\limits_{(1)}\frac{e^{(1-t)s}}{s}ds$$ which is $0$ for $t>1$, $1$ for $t<1$ and $\frac{1}{2}$ for $t=1$.

Question $1$: How does one show that $F(t)=1_{(-\infty,1)}(t)+\mathcal{O}((1+\vert1-t\vert\log x)^{-10})$?

I'm not familiar with Littlewood-Paley theory. A link or reference where something similar is calculated would be appreciated as well.

Question 2: How do I show that $\sum\limits_{p\text{ prime}}\frac{\log p}{p(1+\vert\log \frac{p}{x} \vert)^{10}}$ is bounded uniformly for $x\geq1$ (convergence is clear)?

I think one can show the above by splitting the sum into $3$ bits, one where $p$ is small compared to $x$, one when $p$ is big and one when $p$ is around $x$. I'm having trouble dealing with the terms when $p$ is of size about $x$.

Answer 1

Referring to the comments on the main question above, I am posting my "too long for comments" answer.

I did not thoroughly read through the material in the link provided by the OP in detail to understand the whole background. As such, I am wring my detailed comments with just the OP provided in the text of their question.

1. A smooth roll-off function is achieved with a transition function. You can make your $\Psi(y)$ with a Bump Function constructed out of a transition function. See Here. Note that bump functions are only smooth - they are not analytic. So my initial comment of contour closing is meaningless with any bump function. My initial suggestion of raised-cosine is not even smooth (but only continuous). So that is to be disregarded.

2. Since your question is only dealing with Big-O representation of the integral, we can quickly evaluate the integral with a piecewise function WITHOUT a smooth roll-off. Though the actual integral will not be the same, the order of the terms should not change much. In that spirit, we can approximate $\Psi(y)$ as a piece-wise function as shown below (using $a$ instead of $\epsilon$):

$$ \Psi(y) = \begin{cases} \frac{2}{a} (y+a), & -a \le y \lt -\frac{a}{2} \\ 1, & -\frac{a}{2} \le y \le \frac{a}{2} \\ -\frac{2}{a} (y-a), & \frac{a}{2} \lt y \le a \\ 0, & \text{otherwise} \end{cases} $$

3. As noted in #1 above, contour integration doesn't apply. So we will simply solve this integral in straightforward way.

$$F(t) = \frac{1}{2 \pi i} \int\limits_{(1)} \frac{e^{(1-t)s}}{s} \Psi\left(\frac{\mathfrak{I}(s)}{\log(x)}\right) ds$$

Let's set $s = 1+i p$.

$$F(t) = \frac{1}{2 \pi} \int\limits_{p=-\infty}^{\infty} \frac{e^{(1-t)(1+i p)}}{1 + i p} \Psi\left(\frac{p}{\log(x)}\right) dp$$

Let's set $y = \frac{p}{\log(x)}$.

$$F(t) = \frac{\log(x)}{2 \pi} \int\limits_{p=-\infty}^{\infty} \frac{e^{(1-t)(1+i \log(x) y)}}{1 + i \log(x) y} \Psi\left(y\right) dy$$.

let's now plugin the piecewise formula for $\Psi(y)$ as defined in #2. This integral can be calculated manually, but I used Mathematica. The result is this huge expression (I am pasting an image since this is not intended to be a proper answer)

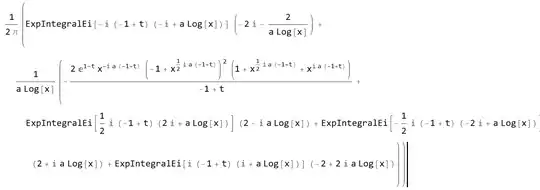
4. If you expand Exponential Integral, you will NOT get terms that are only $O((1+|(1-t)|\log(x))^{-10})$, but you will get much higher order terms, possibly $O(\log(x))+...$. I didn't proceed towards further simplification since your goal is to get that much tighter bound with Littlewood Paley theory. I took a look at it in Wikipedia, but I honestly think that the theory is beyond my current math knowledge.