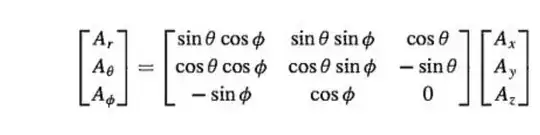0

I have been having trouble understanding vectors in the spherical coordinate system and want to check how far I have got it right.

For a vector $ \vec{r}= A_r\vec{a_r} + A_\phi\vec{a_\phi} + A_\theta\vec{a_\theta} $,

$A_r$ is the length of $ \vec{r} $,

$ A_\phi$ is the angle between the X axis and the projection of $\vec{r}$ on the xy plane,

and $ A_\theta $ is the angle between $\vec{r}$ and the Z axis.

Am I correct so far? So the spherical coordinates of a point P(2, 2, 2$\sqrt{2}$) in the cartesian system, will be (4, $ (\frac{\pi}{4})$, $ (\frac{\pi}{4})$) right?

However, when I use this matrix given by my teacher to convert these coordinates, I get the answer as (4,0,0). What have I understood incorrectly? Matrix for transforming cartesian system vectors to spherical coordinate system vectors

Pumpkin_Star
  • 269
  • Points transform differently from components of vectors. As far as that point is concerned you are probably right (didn't check) . About the vector your teacher is right. – Kurt G. Aug 25 '24 at 12:58
  • Thank you for replying. But I do not understand the first statement. Can't my original point (2,2,root2) be treated as a displacement vector between two different points? – Pumpkin_Star Aug 25 '24 at 13:18
  • You should pick up a differental geometry book from which you will only have to take the definition of a tangent vector., Then you should try to realize that you are confusing $M$ with $T_0M.$ Concrete transformation exercices like this are highly recommended. – Kurt G. Aug 26 '24 at 05:58
  • Thank you very much! I have just got out of highschool and do not know anything about matrices besides basic things like finding the transpose and multiplication. We were given this matrix directly to learn without knowing what transformations are in general or about position vectors vs vectors or how this transformation is not valid for points. I will definitely pick up that book and try to understand it. Meanwhile can you please mention any prerequisites I will need to cover before delving into the transformation exercises you mentioned. I am very grateful for your help. – Pumpkin_Star Aug 26 '24 at 06:21
  • Calculus in several variables is the most important prerequisite. – Kurt G. Aug 26 '24 at 07:47
  • @Pumpkin_Star I don't know what happened to the comment you left in my answer but I suggest reading https://www.physicsforums.com/threads/how-to-define-vectors-in-spherical-coordinate-system.1058560/ to clear your doubts. The main concept here is that the unit vectors change depending on the coordinate of the unit sphere, namely, depend on $(\theta,\phi)$. – Hug de Roda Aug 26 '24 at 16:59

1 Answers1

1

We can deduce geometrically that $$ \begin{pmatrix} \boldsymbol e_r\\ \boldsymbol e_\theta\\ \boldsymbol e_\phi \end{pmatrix} = \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix} \begin{pmatrix} \boldsymbol i\\ \boldsymbol j\\ \boldsymbol k \end{pmatrix} $$ Furthermore, we know that the vector is invariant under change of coordinates and therefore the cartesian and spherical vectors are equal: $$\begin{aligned} \boldsymbol{A_x}&=(A_x, A_y, A_z) \begin{pmatrix} \boldsymbol i\\ \boldsymbol j\\ \boldsymbol k \end{pmatrix}\\ &= (A_x, A_y, A_z) \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix}^{-1} \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix} \begin{pmatrix} \boldsymbol i\\ \boldsymbol j\\ \boldsymbol k \end{pmatrix}\\ &= (A_r, A_\theta, A_\phi) \begin{pmatrix} \boldsymbol e_r\\ \boldsymbol e_\theta\\ \boldsymbol e_\phi \end{pmatrix}=\boldsymbol{A_r} \end{aligned}$$ Since the spherical coordinates are orthonormal this means the change of basis matrix satisfies $\mathbf R\,\mathbf R^\top=1\!\!1$, namely, $\mathbf R^\top=\mathbf R^{-1}$. Thence, $$ \begin{aligned} \begin{pmatrix} A_r\\ A_\theta\\ A_\phi \end{pmatrix} &=\left((A_x, A_y, A_z) \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix}^{-1}\right)^\top\\ &=\left((A_x, A_y, A_z) \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix}^{\top}\right)^\top\\ &= \begin{pmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0 \end{pmatrix} \begin{pmatrix} A_x\\ A_y\\ A_z \end{pmatrix} \end{aligned} $$ which is what your teacher gave you.

Now let's subtitute $A_x=r\sin\theta\cos\phi$, $A_y=r\sin\theta\sin\phi$ and $A_z=r\cos\theta$ and multiply. This means $$ \begin{aligned} &\begin{aligned} \color{blue}{A_r}&=A_x\sin\theta\cos\phi+A_y\sin\theta\sin\phi+A_z\cos\theta\\ &=r\sin^2\theta\cos^2\phi+r\sin^2\theta\sin^2\phi+r\cos^2\theta\\ &=r\sin^2\theta+rcos^2\theta\color{blue}{=r} \end{aligned}\\ \\ &\begin{aligned} \color{green}{A_\theta}&=A_x\cos\theta\cos\phi+A_y\cos\theta\sin\phi-A_z\sin\theta\\ &=r\sin\theta\cos\theta\cos^2\phi+r\sin\theta\cos\theta\sin^2\phi-r\sin\theta\cos\theta\\ &\hspace{0.1cm} \color{green}{=0} \end{aligned}\\ \\ &\begin{aligned} \color{red}{A_\phi}&=-A_x\sin\phi+A_y\cos\phi\\ &=-r\sin\theta\cos\phi\sin\phi+r\sin\theta\sin\phi\cos\phi\\ &\hspace{0.1cm} \color{red}{=0} \end{aligned} \end{aligned} $$ This is why when you inputted the point $\mathsf P(2,2,2\sqrt 2)$ you got $(||\mathsf P(2,2,2\sqrt 2)||,0,0)=(4,0,0)$. In fact, any position vector/point can be described by $r\,\boldsymbol e_r(\theta,\phi)$.

Hug de Roda
  • 4,060