Yes, the expected volume can be given in closed form, with the help of a generalization of Sylvester's Four-Point Problem.
The general term for members of the series (point, line, triangle, tetrahedron, ...) is simplex. The volume of an n-simplex can be easily calculated from a determinant constructed from the coordinates of its vertices, divided by n factorial.
We can calculate the expected volume of a random n-simplex in a unit hypersphere via equation (3) from the linked MathWorld page. We also need the equation for the volume of the unit n-dimensional hypersphere:
$$V(n) = \frac{\pi^{n/2}}{\Gamma(n/2+1)}$$
where $\Gamma()$ is the gamma function. For all $z$, $$\Gamma(z+1) = z\Gamma(z)$$
For non-negative integer $n$,
$$\Gamma(n) = (n-1)!$$
and
$$\Gamma(n+\frac12) = \left(\frac{(2n)!}{4^n n!}
\right)\sqrt{\pi}$$
Note that $V(0)=1$.
The Sylvester equation uses the binomial coefficient, in particular, the generalized central binomial coefficient, which can be written in terms of the gamma function:
$$\binom{2n}{n} = \frac{\Gamma(2n+1)}{\Gamma(n+1)^2}$$
The equation for the expected simplex volume is:
$$S(n) = \frac{\dbinom{(n+1)}{(n+1)/2}^{n+1}}{2^n\dbinom{(n+1)^2}{(n+1)^2/2}} \frac{\pi^{n/2}}{\Gamma(n/2+1)}
$$
Here are the results for small $n$, computed using SageMath:
Exact expected volume
| n |
Expected volume |
| 0 |
$1$ |
| 1 |
$\frac{2}{3}$ |
| 2 |
$\frac{35}{48 \, \pi}$ |
| 3 |
$\frac{12}{715} \, \pi$ |
| 4 |
$\frac{676039}{7776000 \, \pi^{2}}$ |
| 5 |
$\frac{32000}{272254059} \, \pi^{2}$ |
| 6 |
$\frac{107492012277}{27536588800000 \, \pi^{3}}$ |
| 7 |
$\frac{21008750000}{56100739008446649} \, \pi^{3}$ |
| 8 |
$\frac{109701233401363445369}{1210054852352102400000000 \, \pi^{4}}$ |
| 9 |
$\frac{527046113468915712}{778482596802192849805651985} \, \pi^{4}$ |
To 6 significant figures
| n |
Expected volume |
| 0 |
1.00000 |
| 1 |
0.666667 |
| 2 |
0.232101 |
| 3 |
0.0527260 |
| 4 |
0.00880878 |
| 5 |
0.00116005 |
| 6 |
0.000125897 |
| 7 |
0.0000116113 |
| 8 |
9.30694e-7 |
| 9 |
6.59476e-8 |
Here's the Sage / Python script to do those calculations.
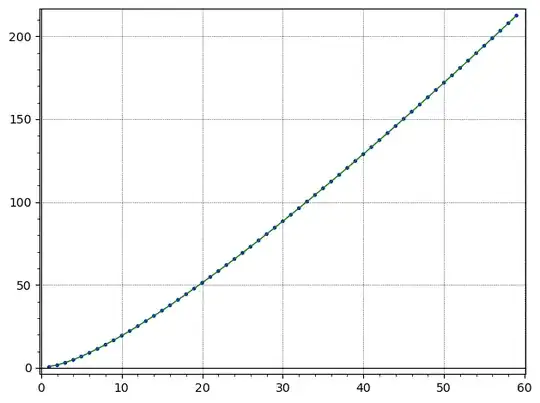
As $n\to\infty$,
$-\log(S(n))$ converges approximately to $$1.322365 - 0.5n + n\log(n)$$
It converges quite quickly. In this plot, the green curve is that function and the blue dots are $-\log(S(n))$.
 Here's the plotting script.
Here's the plotting script.
Here's a Sage / Python script that computes the expected volume by random sampling using the technique given in https://stackoverflow.com/a/54544972/4014959 to generate the uniformly distributed points. The script generates ~500,000 points and then finds the mean of 100 partitions of simplexes formed from those points.
