Product formula for $\dfrac{4}{\pi}$

Question

Can someone give me a hint on how to prove the following formula: $$\frac{4}{\pi}=\left(\prod_{p \equiv 1 \pmod{5} \atop p \in \mathbb{P} } \frac{p}{p+1}\right) \cdot \left(\prod_{p \equiv 2 \pmod{5} \atop p \in \mathbb{P} } \frac{p}{p+2}\right) \cdot \left(\prod_{p \equiv 3 \pmod{5} \atop p \in \mathbb{P} } \frac{p}{p-2}\right) \cdot \left(\prod_{p \equiv 4 \pmod{5} \atop p \in \mathbb{P} } \frac{p}{p-1}\right)$$ where $\mathbb{P}$ denotes set of prime numbers.

Pari/GP code

I think that proof of Euler product formula can be useful but I am not sure. Perhaps some other approach exists.

Answer 1

As something of a ground rule, we might require the factors to be listed in order of increasing value of the prime, so that the different residues $\bmod 5$ are mixed together and thus cancel out, by "interference", the divergent tendencies.

Given a list of consecutive primes starting with $2$, the denominator associated with a prime numerator $p$ is determined by the formula

$2p-5\lfloor(\frac{p}5+\frac{1}{2})\rfloor$

where the second term rounds the prime to the nearest multiple of $5$.

Thus

$2\to(2×2-5×0)=4,3\to(2×3-5×5)=1,$

etc and we get the fractions

$\frac24,\frac31,\frac55,\frac79,...$

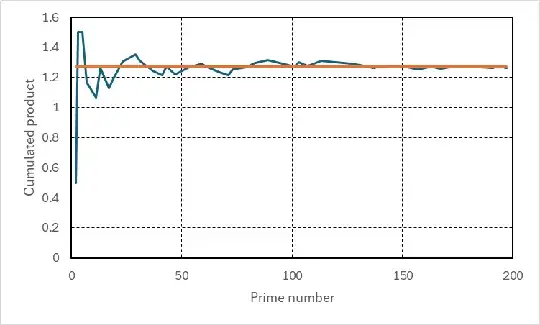
whose cumulated products then seem to be approaching the target value $4/\pi$ indicated by the heavy orange horizontal line:

---

A better established product involving $\bmod 5$ residues of primes is as follows:

$\frac{\pi}{\sqrt5}=+\frac11+\frac13+\frac17+\frac19-\frac1{11}-\frac1{13}-\frac1{17}-\frac1{19}...$

$=(\frac32)(\frac76)(\frac{11}{12})(\frac{13}{14})...$

$=\prod\limits_{p\in\mathbb{P}-\{2,5\}}\dfrac{p}{p+(-1)^{(p+1)/2}(p|5)}$

The infinite series comes from Dirichlet $L$-functions (it may also be derived using a properly constructed Fourier series evaluation). The denominators end with $1,3,7,9$ in base ten and the signs repeat the eight-cycle shown. Converting this to the Euler product form gives the result with the general term indicated in the last line and $(p|5)$ being the Legendre symbol.

Answer 2

Experimental data suggests that the product converges, but to a value less than $4/\pi$. I computed the product for the first $1.8 \times 10^9$ primes. The results are as follows:

• Upto $2 \times 10^7$ primes, product $= 1.27307779$
• Upto $1.8 \times 10^9$ primes, product $= 1.27307727$

and the product has been pretty much flat around this value upto six decimal places without any tendency to increase upto $4/\pi \approx 1.27323954$. The product agrees with $4/\pi$ to only three decimal places so this think this is just a coincidence.

Update 27-Aug: Infact, the data seems to be consistent with

$$ \frac{\pi}{4} = \prod_{p \equiv 1 \pmod{4} \atop p \in \mathbb{P} } \frac{p}{p-1} \cdot \prod_{p \equiv 3 \pmod{4} \atop p \in \mathbb{P} } \frac{p}{p+1}. $$

For the first $10^9$ primes the product agrees with $\frac{\pi}{4}$ to seven decimal places.

Update 29-Aug: My data shows that for any $n \ge 2$ $$ \prod_{r < n \atop p \in P} \left(\prod_{p \equiv r \bmod 2n} \frac{p}{p-1}\right) \cdot \prod_{r > n \atop p \in P} \left(\prod_{p \equiv r \bmod 2n} \frac{p}{p+1}\right)\tag 5 $$ is some algebraic multiple of $\pi$. I have asked this as a separate question here: Product formulas for $\pi$ using prime numbers