0

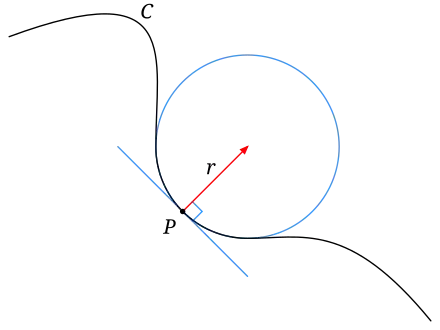
enter image description here

In this image an osculating circle at point P is given. I understand this circle visually as a circle fitting the curve at point P most "snugly". But I want to understand it more clearly through geometry. I can see that the circle is tangent to the point P but there are infinitely many circles tangent to P at that point. Is the osculating circle unique because it is also tangent to points infinitesimally close to P? If so how is that defined mathematically and how would you find the radius of the osculating circle for a parametric curve C(t)?

Gunnar
  • 149
  • 3
  • 2
    Understanding the formula for curvature – Bowei Tang Aug 18 '24 at 02:51
  • @TravisWillse I understand how my question can be similar to that one. I will edit it better clarify that I want to understand property of the osculating circle and how a formula to derive the radius of the osculating circle can be found. – Gunnar Aug 18 '24 at 02:57
  • You can think of a similar process as constructing a tangent line. For the tangent line, you put two points on the curve closer and closer together, and the line passing through both of them approaches the tangent line. Similarly, when you put three points on the curve closer and closer together, the circle passing through all three of them approaches the osculating circle. – Polygon Aug 18 '24 at 03:17
  • @Polygon and given the parametric equation of a curve, how would I derive the formula for the radius of the osculating circle at a point P? – Gunnar Aug 18 '24 at 03:20
  • The linked question and many others have answers saying how to get the radius of curvature from the parameterization of a curve. If you need something different, please edit the question again to clarify what you need. – David K Aug 18 '24 at 03:49
  • @DavidK I don't see any that first define the osculating circle and then derive how to find its radius. All the questions just give the formula of curvature as the magnitude of the derivative of the unit tangent vector and then just say that it is also the inverse of the radius of the osculating circle. I would like a derivation relating to the osculating circle from the geometric definition of an osculating circle. – Gunnar Aug 18 '24 at 03:56
  • What about https://math.stackexchange.com/a/4123391/139123? – David K Aug 18 '24 at 04:04
  • @DavidK is there an answer with more simpler reasoning? I only understand basic vector calculus. – Gunnar Aug 18 '24 at 04:14
  • Is this video the kind of thing you're looking for? It starts with the definition of curvature. Then he uses a circle as a concrete example, and he derives $\kappa = 1/r$. Though he does not derive the location of the center of the osculating circle, it is not too bad, since we now know the circle's radius. – Polygon Aug 18 '24 at 18:04

0 Answers0