What is going on with the discriminant of $f^{\circ n}(X)-X$?

Question

Recently, I found this amazing answer of @Mercio where they point out the following about the discriminant of the polynomial $P(X)=\frac{f^{\circ 3}(X)-X}{f(X)-X}$ where $f(X)=X^2+c$.

We can compute the discriminant of $P$. Amazingly, it's simpler than we should expect, as it factors as $\Delta = (4c+7)^3(16c^2+4c+7)^2$.

I was quite amazed by this. I have been able to compute the following discriminants for $f(X)=X^2+\frac{a}{4}$ (the factor $\frac{1}{4}$ makes the coefficients smaller):

1. $\Delta(f(X)-X)=-(a-1)$
2. $\Delta(f^{\circ 2}(X)-X)=(a-1)(a+3)^3$
3. $\Delta(f^{\circ 3}(X)-X)=(a-1)(a+7)^3(a^2+a+7)^4$
4. $\Delta(f^{\circ 4}(X)-X)=(a-1)(a+3)^3(a+5)^6(a^2-2a+5)^5(a^3+9a^2+27a+135)^{4}$

This is astonishing: whereas $\Delta(f^{\circ n}(X)-X)$ is a polynomial in $\mathbb{Z}[a]$ of degree $n2^{n-1}$, it factors into polynomials of much smaller degree.

One way to compute the last discriminant, is to notice the simple fact that $f^{\circ d}(X)-X$ divides $f^{\circ n}(X)-X$ whenever $d$ divides $n$ and so $$\Delta(f^{\circ 4}(X)-X)=\text{Res}\left(\frac{f^{\circ 4}(X)-X}{f^{\circ 2}(X)-X},f^{\circ 2}(X)-X\right)^2\Delta\left(\frac{f^{\circ 4}(X)-X}{f^{\circ 2}(X)-X}\right) \Delta(f^{\circ 2}(X)-X)$$ where we can compute $$\text{Res}\left(\frac{f^{\circ 4}(X)-X}{f^{\circ 2}(X)-X},f^{\circ 2}(X)-X\right)=(a + 5)^2 (a^2 - 2a + 5)$$ $$\Delta\left(\frac{f^{\circ 4}(X)-X}{f^{\circ 2}(X)-X}\right)=(a+5)^2 (a^2-2a+5)^3 (a^3+9a^2+27a+135)^4$$ This may suggest that there is some sort of recursion with divisibility that explains how to obtain those factors; but I am not really sure how exactly.

My question then is: What is going on here? Why should we expect that these polynomials (of the form $f^{\circ n}(X)-X$ for $f(X)=X^2+\frac{a}{4}$) factor into polynomials of such small degree? What do these small factors mean in this context?

If we work with other polynomials like $g(X)=X^3+\sqrt{\frac{a}{27}}$ or $h(X)=X^3+aX$, it seems that we get the same phenomenon although not as nicely since we have to work with a much rapidly increasing sequence of degrees.

$$\Delta(g^{\circ 3}(X)-X)=\begin{cases}-(a - 4) (a^2+a+ 169)^4 (a^6+162 a^5\\ + 10713 a^4 + 357808 a^3+ 6668064 a^2\\ + 93223104 a + 1235663104)^3\end{cases}$$

$$\Delta(h^{\circ 3}(X)-X)=-2^{26} (a-1)^3(a^2+a+1)^7(4a^2-14a+13)^8H(a)^6$$ $$\text{where }H(a)=\begin{cases}4 a^8+16 a^7-35 a^6- 206 a^5- 113 a^4\\ + 376 a^3+715 a^2+ 1690 a+2197\end{cases}$$

Thanks in advance!

---

Upon further inspection, I have noticed that if we consider a general monic quadratic polynomial $f(X)=X^2+AX+B$, we then have the following relations concerning $\Delta_n:=\Delta(f^{\circ n}(X)-X)$.

2. $\Delta_2 = \Delta_1(\Delta_1-4)^3$
3. $\Delta_3 = \Delta_1(\Delta_1-8)^3(\Delta_1^2-3\Delta_1+9)^4$
4. $\Delta_4=\Delta_1(\Delta_1-4)^3(\Delta_1-6)^6(\Delta_1^2+4)^5((\Delta_1-4)^3-108)^4$

Not only does it seem that $\Delta_n\in\mathbb{Z}[\Delta_1]$ are monic integral polynomials in $\Delta_1$ of degree $n2^{n-1}$, but its factors seem to follow some hidden pattern as well.

Also, if you are interested, the expression for $\Delta_5$ that I have obtained is the following one

5. $\Delta_5=\Delta_1(\Delta_1^4-5\Delta_1^3+10\Delta_1^2+25)^6Q_{11}(\Delta_1)^5$

where the polynomial $Q_{11}(\Delta_1)$ is the following monster $$Q_{11}(\Delta_1)=\begin{cases}\Delta_1^{11} - 42 \Delta_1^{10} + 781 \Delta_1^9 - 8708 \Delta_1^8\\ + 66806 \Delta_1^7 - 379322 \Delta_1^6 + 1642516 \Delta_1^5\\ - 5512992 \Delta_1^4 + 14603953 \Delta_1^3\\ - 30161952 \Delta_1^2 + 47922624 \Delta_1 - 56802816\end{cases}$$

Answer 1

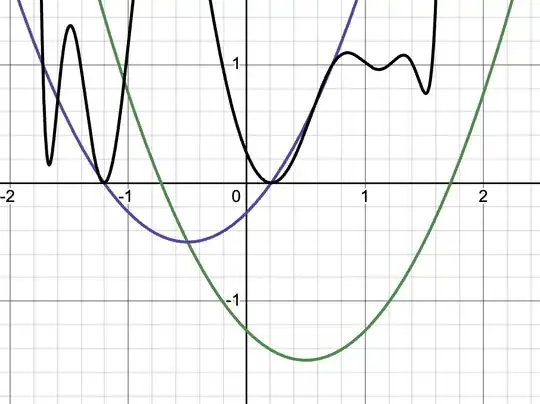
Edit: Here's a graph in Desmos where you can slide the value of $a$ around and see the root collisions at $a = -3$ and $a = -5$ really explicitly. This is what $a = -5$ looks like, where green is $f_1$, blue is $\frac{f_2}{f_1}$, and black is $\frac{f_4}{f_2}$:

---

Write $f_n = f^n(x) - x$ to save on notation. Everything I'm about to do is sloppy and likely could be cleaned up a lot. Also this is all probably somewhere in the literature on arithmetic dynamics.

The roots of $f_n$ are, by definition, $\lambda$ such that $f^n(\lambda) = \lambda$. So they are periodic with period dividing $n$ with respect to the action of $f$. That means they naturally divide up into different classes depending on their period: if $n = 4$ (I am going to focus on this case) they could have periods $1, 2$, or $4$, corresponding to which of $f_1, f_2, f_4$ they are roots of first, and this corresponds to a factorization

$$f_4 = f_1 \frac{f_2}{f_1} \frac{f_4}{f_2}$$

of $f_4$. This factors the discriminant into smaller discriminants and resultants

$$\Delta(f_4) = \Delta(f_1) \text{Res} \left( f_1, \frac{f_2}{f_1} \right)^2 \Delta \left( \frac{f_2}{f_1} \right) \text{Res} \left( f_1, \frac{f_4}{f_2} \right)^2 \text{Res} \left( f_2, \frac{f_4}{f_2} \right)^2 \Delta \left( \frac{f_4}{f_2} \right).$$

Alternately we can work diectly with the discriminant in terms of the product $\prod_{i \neq j} (\lambda_i - \lambda_j)$ over all pairwise differences of roots. These roots live in a finite Galois extension $L$ of the function field $\mathbb{Q}(a)$ (namely the splitting field of $f_n$), and are acted on in two different ways:

• By the Galois group $G = \text{Gal}(L/\mathbb{Q}(a))$; the orbits of this action factor the discriminant over $\mathbb{Q}(a)$.
• By $f$ itself; if $\lambda$ is a root then so is $f(\lambda)$, because $f$ sends periodic points to periodic points.

These actions commute, and they both preserve periods! This means the Galois group must contain and centralize $f$.

If $f(x)$ is quadratic then $f_4$ has degree $2^4 = 16$, so there are $16$ roots $\lambda_i$. They can have periods $1, 2, 4$, and there are $\deg f_1 = 2$ roots of period $1$, $\deg f_2 - \deg f_1$ roots of period $2$, and hence $12$ roots of period $4$. The $2$ roots of period $2$ organize themselves into a single $2$-cycle $\{ \lambda, f(\lambda) \}$ under the action of $f$, while the $12$ roots of period $4$ organize themselves into three $4$-cycles $\{ \lambda, f(\lambda), f^2(\lambda), f^3(\lambda) \}$ under the action of $f$.

$f_1$ and $\frac{f_2}{f_1}$ are both irreducible over $\mathbb{Q}(a)$, so the $2$ roots of period $1$ and the $2$ roots of period $2$ each form a single Galois orbit under the actions of the Galois group of $f_1$ and $\frac{f_2}{f_1}$ respectively. The Galois group of $\frac{f_4}{f_2}$ must contain $f$ acting with cycle decomposition $(4, 4, 4)$, and moreover the action of $f$ commutes with the rest of the Galois group, so the largest the Galois group could be is the wreath product $C_4 \wr S_3$, of order $4^3 \cdot 6$. This means the Galois group acts by permuting the three $4$-cycles and "rotating" each of them individually, although possibly not all such permutations occur.

Now let's analyze the orbits. Write $d(\lambda)$ for the period of $\lambda$ under the action of $f$. We have the following cases for the factors $\lambda_i - \lambda_j$ of the discriminant (of the full polynomial $f_4$ this time):

• $d(\lambda_i) = d(\lambda_j) = 1$. This case occurs twice and we get a single Galois orbit, corresponding to $\Delta(f_1) = - (a - 1)$.
• $d(\lambda_i) = 1, d(\lambda_j) = 2$ or the reverse. This case occurs $8$ times and we get two Galois orbits of size $4$, corresponding to $\text{Res}(\frac{f_2}{f_1}, f_1)^2 = (a + 3)^2$.
• $d(\lambda_i) = d(\lambda_j) = 2$. This case occurs twice and we get a single Galois orbit, corresponding to $\Delta(\frac{f_2}{f_1}) = - (a + 3)$. Together with the above calculation, this is the first example of something we haven't discussed at all, namely: why are there not only so many factors, but why are their multiplicities so high? In this case, why is this $a + 3$ the same as above? This one is easy to understand: what this factor means is that at $a = -3$ the two points of period $2$ have collided. But they have to be sent to each other under the action of $f$. So when they collide their period drops to $1$, and so they also must collide with one of the points of period $1$! And we can check this explicitly: when $a = -3$ the roots of $f_2$ are $\frac{3}{2}$ with multiplicity $1$, and $-\frac{1}{2}$ with multiplicity $3$.
• $d(\lambda_i) = 1, d(\lambda_j) = 4$ or the reverse. This case occurs $24$ times and we get two Galois orbits of size $12$, corresponding to $\text{Res}(\frac{f_4}{f_2}, f_1)^2 = (a^2 - 2a + 5)^2$. This tells us when a point of period $4$ collides with a point of period $1$. I think we get a nontrivial quadratic in $a$ here because this happens at two different values of $a$ depending on which point of period $1$ collides, and we should be able to check this by calculating the roots of $\frac{f_4}{f_2}$ at the two roots of $a^2 - 2a + 5$ and explicitly comparing them with the roots of $f_1$.
• $d(\lambda_i) = 2, d(\lambda_j) = 4$ or the reverse. This case occurs $24$ times and we get two Galois orbits of size $12$, corresponding to $\text{Res}(\frac{f_4}{f_2}, \frac{f_2}{f_1})^2 = (a + 5)^4$ (I think). This tells us when a point of period $4$ collides with a point of period $2$.

The final case $d(\lambda_i) = d(\lambda_j) = 4$ is the most interesting case and is complicated enough that we need to treat it separately. It occurs $12 \cdot 11 = 132$ times and has several Galois orbits, because the points of period $4$ organize into three $4$-cycles as we saw above, and the Galois group is sensitive to whether points are in the same cycle. This corresponds to $\Delta(\frac{f_4}{f_2})$ splitting into different factors, as follows.

• The "generic" case is that $\lambda_i$ and $\lambda_j$ are in different cycles; this case occurs $12 \cdot 8 = 96$ times and is a single Galois orbit. At a value of $a$ at which two points $\lambda_i, \lambda_j$ of period $4$ in different cycles have collided, the same must be true of the points $f(\lambda_i), f(\lambda_j)$, etc.; that is, the rest of the two cycles have also collided, so the discriminant vanishes to order $4$. However, no collisions with points of smaller period have been forced. So this factor of $\Delta(\frac{f_4}{f_2})$ must be the most complicated one, $(a^3 + 9a^2 + 27a + 135)^4$.
• Next, $\lambda_i$ and $\lambda_j$ could be in the same cycle. The next case is that $\lambda_j = f(\lambda_i)$ or $\lambda_j = f^3(\lambda_i)$, which occurs $24$ times and consists of two Galois orbits. At a value of $a$ at which two such roots collide, they become period $1$ and so must also collide with a root of period $1$. That means the corresponding factors of the discriminant must be a power of the factor $a^2 - 2a + 5$ we found in the $(1, 4)$ case above, so I am going to guess that this factor must be $(a^2 - 2a + 5)^3$, although I don't quite understand the multiplicity of $3$.
• The final case is that $\lambda_j = f^2(\lambda_i)$, which occurs $12$ times and is a single Galois orbit. At a value of $a$ at which two such roots collide, they become period $2$ and so must also collide with a root of period $2$. That means the corresponding factors of the discriminant must be a power of the factor $a + 5$ we found in the $(1, 4)$ case above and so must be the remaining factor $(a + 5)^2$.

So, overall this analysis revealed a lot of structure but in the end it turned out the Galois group didn't fully explain the high multiplicities of the factorization (really it only helps explain why $\Delta(\frac{f_4}{f_2})$ splits into three factors but not why their multiplicities are so high), and what we really needed to understand was 1) the behavior of the roots wrt $f$, and 2) the combinatorics of how two roots colliding at different values of $a$ forces other collisions depending on their behavior wrt $f$. Hopefully someone else can clean this up or knows a reference that does all this properly.

Also I might just be wrong about the Galois group and the real Galois group might be smaller, which would break up the factors further.