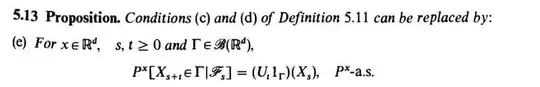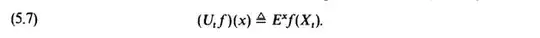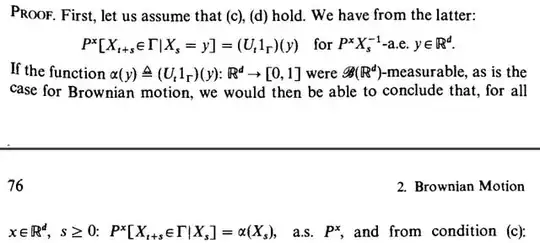I am having trouble understanding part of Proposition 5.13. For context, Proposition 5.13 seeks to prove that in order to show a stochastic process has the Markov property, we can replace conditions (c) and (d) below
with the following condition:
where $U_t$ is defined as below:
However, I am struggling to show the following lines in their proof:
Specifically, the last line, where they state that "if the function $\alpha(y)$ were measurable we would be able to conclude..."
My work: By the definition of conditional probabilities, it suffices to show $$ \int \mathbb{1}_{X_{t + s} \in \Gamma} \cdot \mathbb{1}_{\hbox{arbitrary event in $\mathcal{F}_s$}} d\omega = \int \mathbb{P}^{X_s(\omega)}[Z_{t + s} \in \Gamma] \cdot \mathbb{1}_{\hbox{arbitrary event in $\mathcal{F}_s$}} $$ where $\{Z_{t}\}$ is an independent stochastic process with the same distribution as $\{X_{t}\}$.
Intuitively, (c) implies that the statement holds true for any single value $X_s(\omega) = c$, but how does the author use the measurability of $\alpha(y)$ to extend to arbitrary events in $\mathcal{F}_s$?
Been stuck for a while, so any insight would be deeply appreciated :)