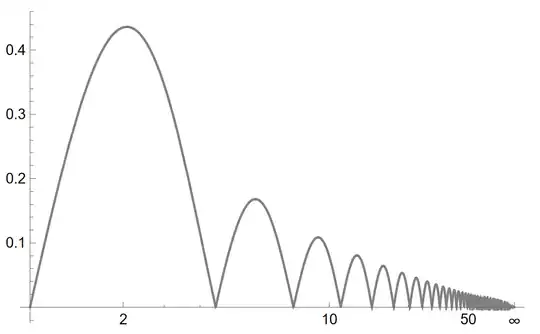
Numerically it appears that the following integral is divergent - I am trying to prove the divergence.
$$\int_0^{\infty } \left| \frac{\cos (t)}{t}-\frac{\sin (t)}{t^2}\right| \, dt$$
There is no singular point of the integrand in the given range (including $0$ and infinity).
By looking at the graph of the integrand below I tend to think that the integral can be shown to be grater than an infinite sum which is divergent. However I am not getting a lead.
Any thoughts?
Hints: $\int_1^{\infty} |\frac {\sin t} {t^{2}}|dt<\infty$. and $\int_0^{1} | \frac{\cos (t)}{t}-\frac{\sin (t)}{t^2}|dt<\infty$ because the integrand tends to $0$ as $ t \to 0$. You only have to show that $\int_1^{\infty} |\frac {\cos t} t|dt=\infty$. This is fairly standard. Look at intervals in which $|\cos t| >\frac 1 2$.
Noticing that $$\displaystyle \left|\frac{\cos t}{t}-\frac{\sin t}{t^2}\right|>\left|\frac{\cos t}{t}\right|-\left|\frac{\sin t}{t^2}\right|, \tag*{}$$ so $$ \int_1^\infty\left|\frac{\cos t}{t}-\frac{\sin t}{t^2}\right|dt> \int_1^\infty\left|\frac{\cos t}{t}\right|dt-\int_1^\infty\left|\frac{\sin t}{t^2}\right|dt $$ The second integral is convergent as $$ \int_1^{\infty}\left|\frac{\sin t}{t^2}\right| d t =-\int_1^{\infty}|\sin t| \frac{1}{t^2} d t <\int_1^{\infty} \frac{1}{t^2} d t =1 $$ For the first integral, we can use method of comparison as @geetha290krm suggested. $$ \begin{aligned} \int_1^{\infty} \left|\frac{\cos t}{t}\right| d t&>\sum_{k=0}^n \int_{(2k + \frac{1}{3} ) \pi}^{(2(k+1)-\frac{1}{3} ) \pi} \frac{|\cos t|}{t} d t \\ & =\frac{1}{2} \sum_{k=0}^n \int _{(2k + \frac{1}{3} ) \pi}^{(2(k+1)-\frac{1}{3} ) \pi} \frac{1}{t} d t\\&= \frac{1}{2} \ln \left(\frac{2}{3}n- \frac{1}{3}\right) \rightarrow \infty \end{aligned} $$ Therefore $\int_1^{\infty} \left|\frac{\cos t}{t}\right| d t$ is divergent and hence $\int_1^{\infty}\left|\frac{\cos t}{t}-\frac{\sin t}{t^2}\right| dt$ is divergent too.
