8

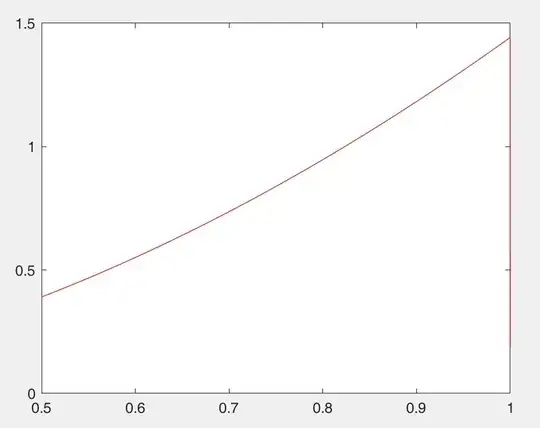
Let the lacunary power series $$f(x):=(1-x)\sum_{n=1}^{\infty}2^{n} x^{2^n},0<x<1.$$ We use Matlab to draw the function $f(x)$ graph, which shows that the function $f(x)$ has limits when $x\to1^{-}$. But we cannot rigorously prove it theoretically. enter image description here

user130405
  • 510
  • I don't understand either of the above two comments. – Adam Rubinson Aug 01 '24 at 11:48
  • 3
    https://math.stackexchange.com/a/3276562 $1/\ln(2)\approx1.44$ – Anne Bauval Aug 01 '24 at 12:27
  • Oh, I see now that it's an integral. I didn't see that before. Thanks – Adam Rubinson Aug 01 '24 at 14:25
  • 1
    Hi @ClaudeLeibovici, as usual you are faster than I am. I can't see the direct relation of the integral in your comment and the sum in the OP. I hope I am not embarrassing myself here, but I have obtained the following: $$\frac12 \sum^\infty_{n=1}2^n x^{2^n} < \int^\infty_0 2^t x^{2^t},dt=\frac{x}{\log 2\log(x^{-1})} < 2\sum^n_{n=0}2^n x^{2^n}$$ but that does not give me (at least I don't see it) the existence of the limit $\lim_{x\rightarrow1-}(1-x)\sum^\infty_{n=1}2^n x^{2^n}$ – Mittens Aug 01 '24 at 17:28
  • @Mittens you should use the upper and lower bounds given by the integral test, and the fact that the function is strictly growing for the existence of the left-side limit – nelynx Aug 03 '24 at 08:52
  • @nelynx: what function? Perhaps you want to write an answer. I am of the opinion that this is a little more than simple calculus, but I'd be interested in seeing in writing what the meaning of your comment. – Mittens Aug 03 '24 at 15:24
  • @Mittens sorry! while writing the answer i realised the integral test cannot be applied here since the sequence in the series is only monotone decreasing after some big enough $n$ which depends on $x$. I'll give it more thought. – nelynx Aug 03 '24 at 23:38
  • 1
    @nelynx: That was what I initially did and found that the problem had more legs… – Mittens Aug 03 '24 at 23:43
  • @ClaudeLeibovici: My answer (found above by Anne Bauval) shows that the limit doesn't exist. After seeing a number of comments later, I've posted yet another answer (below)... – metamorphy Sep 07 '24 at 12:49

1 Answers1

1

An alternative approach (to the mentioned answer of mine).

Let $F(x)=\sum_{n=1}^\infty 2^n x^{2^n}$ and suppose that $L=\lim\limits_{x\to 1^-}(1-x)F(x)$ exists.

Then, after $x=e^{-t}$, we must have $L=\lim\limits_{t\to 0^+}tF(e^{-t})$. Thus $$ G(t):=\lim_{m\to\infty}2^{t-m}F(e^{-2^{t-m}})\qquad(t\in\mathbb{R}) $$ must (exist and) be equal to $L$ independently of $t$. But actually $$ G(t)=\lim_{m\to\infty}\sum_{n=1}^\infty 2^{n-m+t}e^{-2^{n-m+t}}=\sum_{n=-\infty}^\infty 2^{n+t}e^{-2^{n+t}} $$ is a $1$-periodic function whose minimum and maximum on $[0,1]$ are \begin{align} G(0.36110393618947377242\cdots)&=1.44268078066391045448789\cdots \\ G(0.86110352507778026934\cdots)&=1.44270930113294945420168\cdots \end{align} (and there must be an easier way to show that $G$ is non-constant).

metamorphy
  • 43,591