Not understanding or visualizing 4d polytopes at all

Question

In my Euclidean geometry class, one of our final topics was the idea of polytopes, in particular 4D figures. We were told to visualize the hypercube as glued slices of squares, whereas the hypercube is a gluing together of a set of cubes, which is the only visualization I can understand.

However based on the slides, I'm still lost on the notion of a cell. When we intersect a figure with $x_i=\pm1$, what does the 4D equivalent $x_4$ represent based on the drawn figure? What exactly are these 8 "cells" as illustrated on the figure on slide 5? I'm lost.

Answer 1

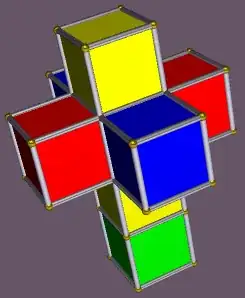
"Cells" here refers to "$3$-dimensional faces," so in the picture the cells are all solid cubes. The easiest one to see in the picture is the little cube in the middle; it's being left hollow but "cell" here is referring to the entire interior of that cube:

                                                    

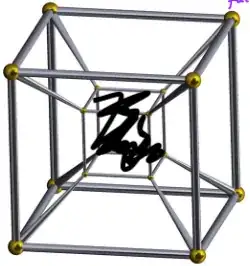
The little cube is also surrounded on each of its $6$ faces by $6$ other squashed cubes (which have a pyramidal shape in the picture, but in the "actual" hypercube these cubes are all the same size and shape). This accounts for $7$ cubes. Here I'm only going to indicate the one on the bottom so the image isn't too messy:

                                                    

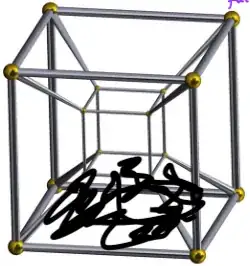
The $8$th cube is the hardest one to see; it is the entire region outside of the big cube, and in particular in this drawing of the hypercube it is infinite. This image is not even fully accurate because strictly speaking this final cube includes the "camera" from which we're viewing this whole thing but if I filled that in this whole image would be black:

                                          

This is, again, not how the "actual" hypercube works; here we're doing a stereographic projection to project the hypercube into 3d. Then that picture is a further projection into 2d! It's amazing that this gives us any meaningful information at all, really.

You can see that together the cubes fill up all of $\mathbb{R}^3$; this is really the $3$-sphere $S^3$ in $\mathbb{R}^4$, minus the point at infinity. This is the 4d analogue of the "spherical" drawing of a cube on a $2$-sphere $S^2$, which looks like this, and which also has a funny stereographic projection into $\mathbb{R}^2$ making one of the faces infinite, which I can't find a good picture of. But it's the 2d analogue of this diagram: a square inside another square, connected by $4$ edges.

Answer 2

If it's still hard for you to go by stereographic projection (as mentioned in the other answer), you might want to go via nets.

Consider the well-known net of a cube from the six squares unfolded into 2D space. Similarily the net of the tesseract is built from 8 cubes and can be unfolded into this 3D thing:

Like for the 3D cube you also would for the 4D tesseract have to re-attach nearby elements piece by piece, eg. the left face of th green cube will have to attach to the left face of the left red cube, while the front face of the green cube will have to attach to the front face of the blue cube, and the bottom face of the green cube will have to attach to the top face of the upper yellow cube.

Note that re-attaching the 2D net into a cubical surface was meant to leave the 2D space and bends into the 3rd dimension. Same holds true for this 3D net of the 4D tesseract: while bending over either cube to attach to the neighbouring cube, you would have to leave the 3D space and bend into the 4th dimension!

--- rk