Informal definition of groups in Nathan Carter's "Visual Group Theory"

Question

Context

In Visual Group Theory by Nathan Carter, the author introduces groups by considering the set of all actions generated by a given collection of actions, which are called generators. In section 1.4, the author lays down the conditions that the set of actions must follow in order to create a group:

Rule 1.5. There is a predefined list of actions that never changes.

Rule 1.6. Every action is reversible.

Rule 1.7. Every action is deterministic.

Rule 1.8. Any sequence of consecutive actions is also an action.

This is followed by Definition 1.9, which states:

Definition 1.9 (group, unofficially). A group is a system or collection of actions satisfying Rules 1.5 through 1.8.

This is explained with an example:

Rubik’s Cube [...] has only six moves - rotating any one of the six faces 90 degrees clockwise. By combining these six moves, players can explore the full (enormous) gamut of cube configurations.

---

Question

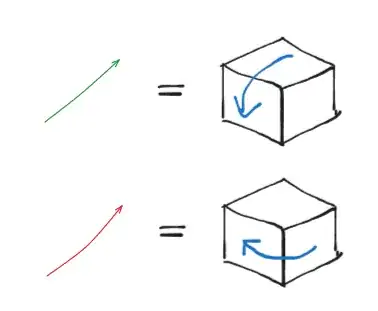
Consider a cube with a dot on one face, and a cross on the face exactly opposite to it.

Consider the following arrows as actions (rotations of the cube) which we are going to use as generators.

These 2 actions (and the ones we get by using them as generators) satisfy all rules from 1.5 to 1.8 (or so it appears to me).

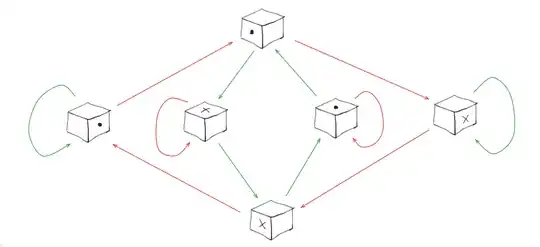
Considering all possible orientations of the cube and the actions that correspond to changes linking one orientation to another, we get the following Cayley graph:

However, the Cayley graph shown above doesn't represent a group, since the red arrow behaves as an identity action over two particular orientations, but not on the other four. (We can say the same for the green arrows too).

It appears we have reached a contradiction, since by Definition 1.9, the generators described above should constitute a group. What am I missing here?

Answer 1

I think the problem lies in formalizing the concept of an action.

In your example, ask yourself: What are the generators acting on?

The answer which resolves your apparent contradiction is: each generator is acting on the full set of six diagrams, namely the six cube diagrams in your picture. One element of that set is: dot on top, cross on bottom (this is the third diagram of the middle row). Another element is: dot on back right, cross on front left (this is the bottom diagram). And so on through the possible markings, just as you have depicted them.

Yes, it is a true fact: the action of the red generator fixes two of the diagrams: the 2nd and 3rd ones in your middle row. But it is also true that the action of the red generator does not fix the other four diagrams, instead it permutes them in a cycle.

The formal idea here is each individual action is a permutation of the specified set. This is how Rule 1.7 can be formalized: we are specifying the full set of six box diagrams, and each action is determined as a permutation of that set. In your example, the red arrows show the permutation of the six diagrams that constitute the red action; and the green arrows show the permutation that constitutes the green action.

To see how this works out in Rule 1.6, that rule says that the inverse of any permutation in the collection is also in the collection. In the case of the red action, to get its inverse, just reverse each and every red arrow; interestingly, exactly two of the arrows of the "red reversed" action are also arrows of the red action itself; but the other four "red reversed" arrows point in the opposite direction of the original red arrows.