1

If $X$={$1,2,3,4$} , how many functions $f:X \rightarrow X$ satisfy the following condition $f(2)\le f(3) \le f(4)$ ?

Note. My approach is as follows:

There are two ways of function selection

Either 1) One to One and 2) Many to One

For one to one, we have the following cases:

enter image description here

Not able to do many to one.

N. F. Taussig
  • 79,074
Samar Imam Zaidi
  • 9,202
  • 2
    There are only $4^4=256$ functions in total. You could make a spreadsheet to make a list of them all, then identify the ones that satisfy your constraint. Or you could adapt stars and bars to show where the increases happen. – Ross Millikan Jul 22 '24 at 03:46
  • What's wrong with "$3$ $1$ $2$ $4$"? – Dominique Jul 22 '24 at 11:57

2 Answers2

1

I am assuming that one-to-one signifies that each of $~f(1), \cdots, f(4)~$ are distinct, and that many-to-one signifies that $~f(1), \cdots, f(4)~$ are not necessarily distinct.

For one-to-one, there are $~\displaystyle \binom{4}{3}~$ ways of choosing the set $~\{f(2),f(3),f(4)\}.~$ Once this set is determined, there is only one way of permuting the elements appropriately. So, the answer, for one-to-one is $~4.$

Many-to-one will yield to analysis.

For $~f(3),~$ there are $~5 - f(3)~$ choices for $~f(4),~$ and there are $~f(3)~$ choices for $~f(2).~$

Therefore, the desired many-to-one computation is

$$4 \times \sum_{f(3) = 1}^4 \left\{ ~f(3) \times \left[ ~5 - f(3) ~\right] ~\right\}. \tag1 $$

In (1) above, the LHS factor of $~4~$ represents that regardless of the choices made for $~f(2), ~f(3), ~$ and $~f(4),~$ there are $~4~$ choices for $~f(1).$

user2661923
  • 42,303
  • 3
  • 21
  • 46
1

I discussed how to count the number of strictly increasing functions and increasing (nondecreasing) functions $f: \{1, 2, 3, \ldots, n\} \to \{1, 2, 3, \ldots, m\}$, where $m \geq n$, here.

In this problem, $f$ is nondecreasing on the subset $\{2, 3, 4\} \subseteq X$. Both the one-to-one and many-to-one cases can be handled at once.

Since there are no restrictions on $f(1)$, its value can be selected in four ways.

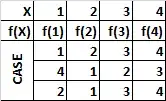
Since $f(2) \leq f(3) \leq f(4)$, the number of ways we can assign $f(2)$, $f(3)$, and $f(4)$ is completely determined by how many of these elements have image $1$, image $2$, image $3$, or image $4$. For instance, if none of these elements have image $1$, one has image $2$, one has image $3$, and one has image $4$, then $f(2) = 2, f(3) = 3,$ and $f(4) = 4$. Similarly, if two of these elements have image $1$ and one has image $2$, then $f(2) = f(3) = 1$ and $f(3) = 2$.

Let $y_1, y_2, y_3, y_4$ be, respectively, the number of elements in $\{2, 3, 4\} \subseteq X$ that are mapped to $1, 2, 3, 4$. Then $$y_1 + y_2 + y_3 + y_4 = 3$$ is an equation in the nonnegative integers. A particular solution to the equation corresponds to the placement of three addition signs in a row of three ones. For instance, $$+ 1 + 1 + 1$$ corresponds to the solution $y_1 = 0, y_2 = y_3 = y_4 = 1$ (and the case $f(2) = 2, f(3) = 3, f(4) = 4$), while $$1 1 + 1 + +$$ corresponds to the solution $y_1 = 2, y_2 = 1, y_3 = y_4 = 0$ (and the case $f(2) = f(3) = 1, f(4) = 2$). The number of such solutions is the number of ways we can place $4 - 1 = 3$ addition signs in a row of $3$ ones, which is $$\binom{3 + 4 - 1}{4 - 1} = \binom{6}{3}$$

Since there are four ways to assign the value of $f(1)$ and $\binom{6}{3}$ ways to assign the values of $f(2), f(3), f(4)$ such that $f(2) \leq f(3) \leq f(4)$, the number of functions $f: X \to X$ such that $f(2) \leq f(3) \leq f(4)$ is $$\binom{4}{1}\binom{6}{3}$$

Note: In your table of admissible one-to-one functions, you overlooked the case $f(1) = 3, f(2) = 1, f(3) = 2, f(4) = 4$.

N. F. Taussig
  • 79,074