I'm trying to fully understand the cut property in the concept of minimum spanning trees (MST) in graph theory and graph algorithms. It seems that all the literature out there proves this theorem via contradiction, which is extremely irritating because it does not help for my intuition. I've been trying to draft a direct proof with little success, or just half-way.
I'll formalize:
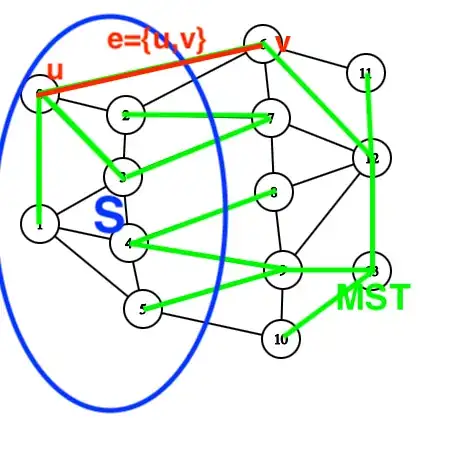
Theorem: We have an undirected, weighted, connected graph (with positive weights) $G=(V,E,\omega)$. For any arbitrary cut $(S,V\backslash S)$ the cutting edge $e$ with the minimum weight ($e:=\underset{v\in E\bigcap(S\times(V\backslash S))}{min}\left\{ \omega(v)\right\}$) will be part of all MST's of G.
Proof: I'd like to prove it with the above example as a visual "general case", since I feel all the proofs out there always show an example that is not general enough (e.g. the sub-MST's on each side are inside the cut). My original idea is to go by analyzing two possible cases:
- $e$ belongs to all MST, in which case removing it from the MST's would always yield two sub-trees departing from $u$ and $v$ respectively.
- $e$ does not belong to any MST, in which case one could find a way from $u$ to $v$ without using $e$ within the MST.
We then prove that 2. is not possible. The problem is that there exist cut-edges in that cut $S$ that belong to the MST and that confuses me. How should I proceed?
Thank you.