Discretized Distributions on Rationals?

Question

Consider the measure space $(\mathbb{Q}, 2^{\mathbb{Q}}, \nu)$, with $\nu$ being the counting measure. The space is then $\sigma$-finite. Is there any attempts made to define analogues of continuous distributions on this space such that, when we sample from it (assuming we can), it shall look empirically like the corresponding continuous distribution? For example, can we define $N(0,1)$ on rationals? The problem is to find a density $f$ with respect to $\nu$ such that $\sum_{x \in \mathbb{Q}}f(x)$ makes sense. The traditional $\sum_{x \in \mathbb{Q}} e^{-\frac{x^2}{2}}$ does not seem to be working.

Answer 1

Expanded from comments:

I do not see how you plan to sum (as opposed to integrate) a density (as opposed to a probability mass function) and get 1. You could create an discrete distribution on the rationals which is arbitrarily close to $N(0,1)$ in a CDF sense, but it would not be equal to it.

As an example,

• choose some positive integer $c>\frac1\epsilon$,
• consider all the positive rationals with denominator $\le c$,
• list them in the usual order (so for example $q_1=\frac1c, q_2=\frac1{c-1}, \ldots$ and there are a finite number between any pair of integers),
• let $q_0=0$ and $q_{-i}=-q_i$.
• Then say $\mathbb P(X=q_i)=\Phi\left(\dfrac{q_{i+1}+q_i}{2}\right) - \Phi\left(\dfrac{q_{i}+q_{i-1}}{2}\right)$ and your CDF will be close to that of $N(0,1)$.

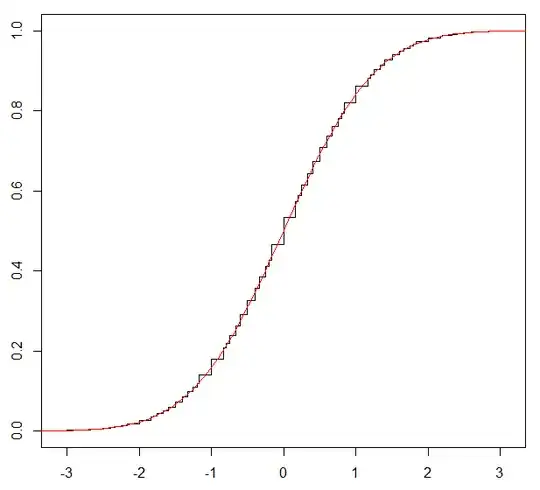
Here is an illustration when $c=6$ so the ordered rationals include $\cdots, -\frac12, -\frac25,-\frac13,-\frac14,-\frac15,-\frac16, \frac01, \frac16,\frac15,\frac14, \frac13, \frac25, \frac12, \frac35,\frac23,\frac34,\frac45,\frac56, \frac11, \frac76,\cdots$.

The CDF (in black, compared to the continuous $N(0,1)$ in red) looks like this and has a maximum error less than $0.03321$.

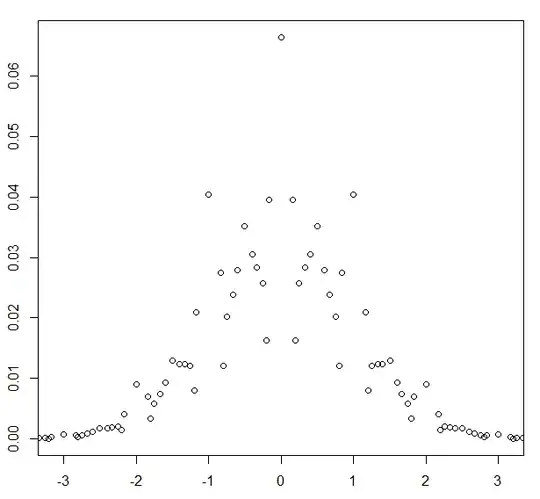
The corresponding probability mass function looks like

and you can sum these values as you wish, since there are a countable number of positive probabilities; overall the sum of probabilities will be $1$ as desired. It is not a density.

The issue is that as $\epsilon$ decreases and $c$ increases, these probabilities will each tend towards $0$, so there is not a useful limit.

Answer 2

I would say that "nice", "benchmark" continuous disributions tend to have regular supports - closure of the set on which its density (w.r.t. the Lebesgue measure) is positive. E.g. a uniform distribution is supported on an interval, exponential distribution is supported over a half-line and normal distribution has the whole real line as its support. In particular over the corresponding supports their densities are positive and continuous everywhere hence over each compact subinterval of their respective supports their densities attain the minimal value $\delta > 0$.

Recall however that if you take a countable number of values each above $\delta>0$, their sum will be infinite. On the other hand, any open interval of a real line contains a countable number of rationals. As a result, any probability distribution over rationals will have the property that $\inf_{a< r < b}p(r) = 0$ where the sum is taking over all rational numbers in an interval $(a, b)$ and $p$ is the probability mass function of your distribution.

So no matter where and how small you pick the open interval $(a, b)$, it will have a subsequence of rational numbers over which the probabilty mass function tends to zero. Unless you just let this function to be non-zero at a finite number of points within each such interval (see e.g. Henry's answer), you will get a function that looks rather unpleasant, definitely unlike anything that resembles uniform, exponential or normal densities.