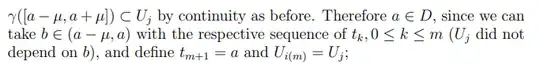1

I have been trying to get my head around this question and its solution.

The (easier and more straightforward) solution using the Lebesgue Number Lemma is greatly explained here: Prove that a space is simply connected

Let $X$ top. Space and $x_0 \in X$. Let $(U_i)_{i \in I}$ be open sets in $X$, $\quad$ $x_0 \in U_i \forall i$, $\quad$ $X = \cup \space U_{i}$ and $U_i \cap U_j$ is path-connected for all $i$ and $j$ in $I$.

Let $\gamma: [0, 1] \to X$ be a loop at $x_0$. Show $\exists m \geq 1$ and real numbers $[t_0 = 0 < t_1 < \cdots < t_{m-1} < t_m = 1]$ such that for $0 \leq k < m$, the subset $\gamma([t_k, t_{k+1}])$ is contained in $U_{i(k)}$ for some $i(k) \in I$. (1)

The solution given was essentially this: Let $D = \left\{ \delta \in (0, 1] : \exists m \geq 1 \text{ and } 0 = t_0 < \cdots < t_m = \delta \text{ with property (1)} \right\}.$ We prove that $D$ is open and closed which implies $D$. Now the trouble starts. Essentially I have to main questions:

  • Why does D beeing clopen imply that we solved the problem?
  • How do I prove D is closed

The solution provided:

enter image description here enter image description here

This may be trivial but I somehow have a hard time understanding this so I would be grateful for an explanation.

manifold97
  • 77
  • 1
    The suggested proof is unnecessarily complicated. Instead, use the Lebesgue lemma on existence of a Lebesgue number for an open cover of a compact metric space (the unit interval in this case). – Moishe Kohan Jul 14 '24 at 13:59
  • @MoisheKohan Thank you. Forgot about this Lemma, recalled it and was very straightforward from there. – manifold97 Jul 15 '24 at 09:08

1 Answers1

1

$D$ being clopen implies it is all of $(0, 1]$ since $(0, 1]$ is connected, and $D = (0, 1]$ is in particular to say that the statement holds for $\delta = 1$ which is what you're trying to show.

As for closedness, I think the proof you showed is quite cumbersome, so here's a somewhat simplified argument:

I'm going to pick up the proof at "if it $D$ is not closed, then it is of the form $(0, a)$." We're going to show that in this case it already holds that $a \in D$, contradicting the fact that it isn't closed.

Choose $j \in I$ such that $\gamma(a) \in U_j$. We claim that for some $b \in D$, $\gamma([b, a])$ is already a subset of $U_j$, at which point we're done: Since $b \in D$, we can take a partition $0 = t_0 < \ldots < t_m = b$ with the desired property and extend it by $t_{m + 1} = a$, so that $a \in D$ as well.

But this is clear: $U_j$ is open, so $\gamma^{-1}(U_j)$ is open (as $\gamma$ is continuous). In particular, $\gamma^{-1}(U_j)$ contains an open interval around $a$, which then in turn contains a closed interval $[b, a]$ for some $b \in D$.

Ben Steffan
  • 8,325