The center of gravity of a triangle on a parabola lies on the axis of symmetry

Question

About an hour ago, I discovered a beautiful property of a parabola. 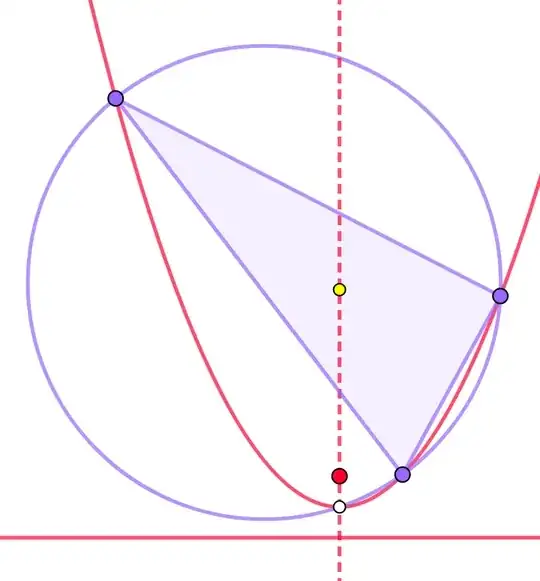If a circle intersects a parabola at four points, one of which is the vertex of the parabola, then the center of the triangle, whose vertices are the remaining three points, will belong to the axis of symmetry of the parabola

Is this feature known in advance or not, please mention any references that talk about the topic

I haven't tried to prove it yet, but I don't expect that to be difficult using analytic geometry, but evidence is welcome in the answers.

I want to point out that I have been inspired by theorem 11.3.15 in Arseny Akopian's book — زكريا حسناوي, Jul 09 '24 at 19:16
This is related to a property of concyclic points on a parabola: if we place the parabola in a coordinate system that renders it as $y=kx^2$, then four points on the parabola are concyclic iff their $x$-coordinates sum to zero. — Oscar Lanzi, Jul 09 '24 at 22:24
It seems worth linking to Oscar Lanzi's own question on the subject: https://math.stackexchange.com/questions/4753014/prove-four-points-on-a-parabola-are-concyclic. — Semiclassical, Jul 09 '24 at 22:40

Semiclassical · Accepted Answer · 2024-07-09T19:58:06.227

11

We can prove a stronger claim, namely that this works for any axis-aligned ellipse which passes through the parabola vertex. First, we choose coordinates such that the parabola's vertex is $(0,0)$ and thus the parabola is of the form $y=ax^2$. Then the equation of a generic ellipse which passes through the origin is $$A(x-h)^2+B(y-k)^2=Ah^2+Bk^2$$ The intersection of this circle with the parabola is now found by solving

$$A(x-h)^2+B(ax^2-k)^2=Ah^2+Bk^2$$ for $x$. Eliminating the trivial solution $x=0$, we get the cubic $$a^2 B x^3+(A-2akB)x-2Ah=0$$ The lack of a quadratic term in this cubic means that the three roots $x_1,x_2,x_3$ sum to zero. Hence the $x$-coordinate of the center of mass of the points $\{(x_k,y_k)\}_{k=1}^3$ is $\frac13(x_1+x_2+x_3)=0$ which indeed falls on the axis of symmetry.

edited Jul 09 '24 at 19:58

answered Jul 09 '24 at 19:43

Semiclassical

18,592

Very interesting! Do you recommend any not too advanced textbook for conical surfaces? – Francisco J. Maciel Henning Jul 09 '24 at 20:08
After some experimentation, this is as far as the statement seems to able to go: if we use a generic ellipse (not axis-aligned) then the resulting cubic after imposing $y=ax^2$ can and will have a quadratic term, which contradicts the claim. – Semiclassical Jul 09 '24 at 20:09
@FranciscoJavierMacielHennin Can't say I do: the above is just based on algebra and not any particular textbook. – Semiclassical Jul 09 '24 at 20:10
Oh, thank you anyway. – Francisco J. Maciel Henning Jul 09 '24 at 20:14
As an aside, the case of an axis-aligned ellipse is not actually too much stronger than the original form: we can always rescale the axes to convert such an ellipse into a circle, in which case the original statement suffices. – Semiclassical Jul 09 '24 at 20:15
@FranciscoJavierMacielHennin You can start with Coordinate geometry by SL Loney as an intro. – An_Elephant Jul 10 '24 at 04:50
Thank you! I will – Francisco J. Maciel Henning Jul 11 '24 at 03:34
In fact, it turns out that the property generalizes to a conic segment whose axis of symmetry is parallel to the axis of symmetry of the parabola, showing that the theorem still works if we use hyperbola instead of an ellipse or a circle. – زكريا حسناوي Jan 06 '25 at 04:11

The center of gravity of a triangle on a parabola lies on the axis of symmetry

1 Answers1