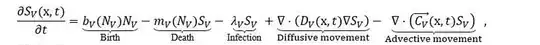I am working on a "reaction-advection-diffusion" type epidemiological model using a system of partial differential equations (PDEs). From this PDE model, I would like to numerically compute the basic reproduction number (R0) to represent its relationship with the diffusion and advection terms.
I calculated R0 numerically for the ordinary differential equations (ODEs) of my model using the dominant eigenvalue of the next-generation matrix, K, which is given by 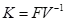 (where the matrices F and V are defined from the partial derivatives of matrices capturing the rates at which new infections occur in the infection compartments and the rates at which individuals move among the infection compartments, respectively).
(where the matrices F and V are defined from the partial derivatives of matrices capturing the rates at which new infections occur in the infection compartments and the rates at which individuals move among the infection compartments, respectively).
Is there a method available to numerically compute R0 for PDE models? Any advice or even just a link towards a reference would be greatly appreciated.