0

I don't understand what the angle "t" is in the parametric equation of an ellipse.

The parametric equation from books is given as:

$$x = a\cos t$$ $$y = b\sin t$$

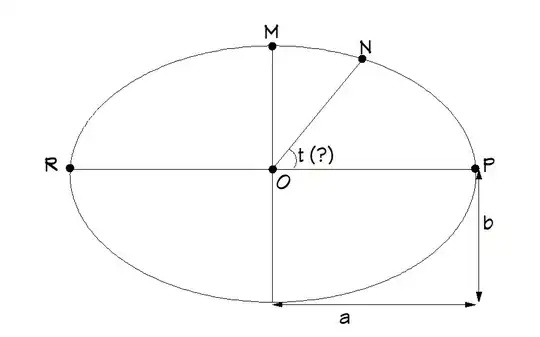
Referring to the diagram, isn't "t" equal to the angle shown on the diagram? I mean if "t" = $0$ then the x value for point P is a and y is equal to $0$, which are correct and if "t" = $90$ degrees, then the x value for point M is $0$ and y value is b.

If the angle shown on the diagram is not "t", then what is "t"? Also, what if I am given the angles of the points on the ellipse. For example Point P is $0$, N is $67$, M is $90$ and R is $180$. Can't I just assume that these are equal to t and use the equations that I listed above to solve for x and y?

enter image description here

rdemo
  • 413
  • In the section titled "Parametric representation", of the link below, the writers claim that "t" is not the angle of (x(t), y(t)) with the x-axis, but has geometric meaning due to Philippe deLa Hire. I am confused because the angle to B in their diagram is different than the angle to P on the ellipse. "t" is shown as the angle to B on the circle.

    https://mathresearch.utsa.edu/wiki/index.php?title=Equation_of_an_Ellipse

     – rdemo Jul 01 '24 at 03:25
  • As a followup: If "t" is equal to the angle shown for the circle in the link that I posted in the comment above and if we change "t" to "q" in my diagram of the original post, how would I relate "t" for the parametric equations (which seem to be based on the circle shown in the link) to "q" so that I can use the parametric equations. – rdemo Jul 01 '24 at 03:34
  • 2
    In the geometric description, points $A$ and $B$ on the "outer" and "inner" circles each make angle $t$ w/the $x$-axis. From $A$ and $B$, we construct $P$ that traces the ellipse; since $A$, $B$, $P$ are almost-never collinear (for $a\neq b$), the angle $P$ makes w/the $x$-axis (call it $p$) almost-never matches $t$. Anyway, the resulting parameterization of $P$ is $(a\cos t,b\sin t)$, so we have $$\tan p=\frac{P_y}{P_x}=\frac{b\sin t}{a\cos t}=\frac{b}{a}\tan t$$ To get $p$ from $t$ or vice-versa, use $$p=\operatorname{atan2}(a\cos t,b\sin t)\qquad t=\operatorname{atan2}(b\cos p,a\sin p)$$ – Blue Jul 01 '24 at 04:15
  • I'm sorry, I don't understand what $atan2(acost,bsint)$ means. I've only ever seen atan and I've never seen a comma in the argument for atan. – rdemo Jul 01 '24 at 05:17
  • Easy enough to look it up: https://en.wikipedia.org/wiki/Atan2 – David K Jul 01 '24 at 05:23
  • If what you want is an equation for an ellipse in the form $r=f(\theta)$, that is, when $\theta$ is the angle $\angle PON$ then $r$ is the distance from $O$ to $N$ -- here's a derivation of the formula: https://math.stackexchange.com/a/1607673/139123 – David K Jul 01 '24 at 05:25
  • The point of a parametric equation is typically that it doesn't require you to be able to express one coordinate as a function of the other, either in Cartesian or polar coordinates. It's perfectly usable for many purposes. If it's not usable for your purposes, you might get an answer if you explained what you really need. – David K Jul 01 '24 at 05:27
  • @rdemo: See Wikipedia's "Atan2" entry. Briefly: $atan2(x,y)$ gives the angle the point $(x,y)$ makes with the $x$-axis; eg, $$atan2(1,1)=45^\circ\quad atan2(-1,1)=135^\circ\quad atan2(-1,-1)=-135^\circ\quad atan2(1,-1)=-45^\circ$$ Compare this to $\arctan(y/x)$, which loses quadrant information, returning only angles between $-90^\circ$ and $90^\circ$: $$\arctan\frac{1}{1}=\arctan\frac{-1}{-1}=45^\circ \qquad \arctan\frac1{-1}=\arctan\frac{-1}1=-45^\circ$$ So, $atan2$ is better suited to converting between angles $p$ and $t$ mentioned in my comment. – Blue Jul 01 '24 at 06:01
  • If you need the polar angle as parameter, then use the polar equation of the ellipse: https://en.wikipedia.org/wiki/Ellipse#Polar_form_relative_to_center – Intelligenti pauca Jul 01 '24 at 14:19
  • $t$ is known as an eccentric angle of the auxiliary circle of an ellipse. – Ng Chung Tak Jul 03 '24 at 10:35
  • For a centre-origin ellipse in polar coordinates, $$r(\theta)=\frac{a b}{\sqrt{a^2\sin^2 \theta+b^2\cos^2 \theta}}$$ – Ng Chung Tak Jul 03 '24 at 10:39

0 Answers0