How can I convert Interval Difference to Circle of Fifths segments and position

Question

How to convert Interval Difference to Circle of Fifths segments and position

Hi, Im designing a numeric decimal notation code model for exploring math relations between notes on chromatic scales and circle of fifths.

The model uses numeric identifiers instead of letters. So for example "G" is represented as " 1.50 ".

Have a problem which Im guessing is likely easy for most of you out there well versed in music theory - would love feedback on this and pointers to a solution. My hope is to end up with a simple straight forward math formula / function that can be used.

Description ; Given two musical notes, determine the distance between note 1 and note 2 on a standard scale, 7 or 12 based scale and then convert this distance to the number of segments on the circle of fifths separating the values.

For example, here we have two notes ;

NOTE 1 = 1.483 ( G ) NOTE 2 = 1.428 ( F # )

Distance between n1 : n2 = 1.93 ( B # )

where ; 1.483 * 1.93 = 1.428

Using this value of 1.93, we want to derive the number of segments that separate NOTE 1 & NOTE 2 on the circle of fifths, which is 4.0

The notes are assigned their numerical values ( not lettered names ), so for example instead of labelling the note "G", here the decimal numeric equivalent is used such that ; 2^(7/12) = 1.5, in the case of the examples given ; 1.48 ~ ( 2^(6.82/12) ), and 1.428 ~ (2^(6.16/12)), the note values given are irregular

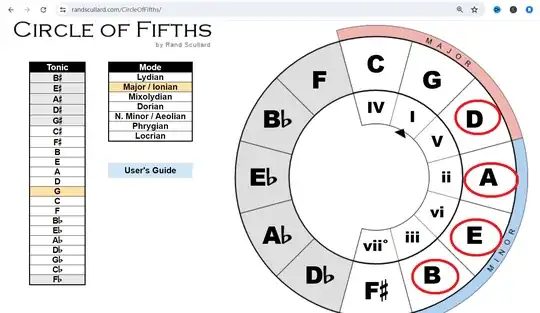
If I look visually at the circle of fifths such as via this link ; https://randscullard.com/CircleOfFifths/ and from the left column labelled "Tonic" click on the G note, I can see that the "F#" is four segments clockwise from the "G"

Each segment has the equivalent of 7 semitones to equal a p 5th and 1.496^11 = 7 * 12

But the function, formula I am hoping for is one where I can input the distance between two notes and get as an output the equivalent number of segments of the circle, in the case of the above example this should be ;

1.93 = 4.0

Where 1.93 is the distance on a scale between note 1 and note 2 and 4.0 is the distance between the notes on the circle of fifths. The math function should use the values of note 1, note 2, distance ; 1.48, 1.428, 1.93, to compute the number of segments on the circle ; 4.0

Can anyone provide some direction on this?

Much thanks

D

Answer 1

If I understand your system correctly, your numbers are just the 12-ET frequency ratio relative to C, i.e.,

• C = $1$
• C♯/D♭ = $2^{1/12} \approx 1.059$
• D = $2^{1/6} \approx 1.122$
• D♯/E♭ = $2^{1/4} \approx 1.189$
• E = $2^{1/3} \approx 1.260$
• F = $2^{5/12} \approx 1.335$
• F♯/G♭ = $2^{1/2} \approx 1.414$
• G = $2^{7/12} \approx 1.498$
• G♯/A♭ = $2^{2/3} \approx 1.587$
• A = $2^{3/4} \approx 1.682$
• A♯/B♭ = $2^{5/6} \approx 1.782$
• B = $2^{11/12} \approx 1.888$

To find the interval between two notes, first find the number of semitones between them. If $x$ is the lower note and $y$ is the higher one, then:

$$\boxed{s = 12\log_2\left(\frac{y}{x}\right)} \approx 17.31234\ln\left(\frac{y}{x}\right)$$

For example between F and B, we have:

$$s = 12\log_2\left(\frac{1.888}{1.335}\right) \approx 6$$

You'll want to round to the nearest integer to account for rounding errors in the frequencies.

---

Now, on to the Circle of Fifths.

In the original version of this answer, I gave the formula $\boxed{f = (7s) \bmod 12}$ (where $f$ is the number of fifths, and $s$ is the number of semitones), but that only works for 12-ET. So, I'll generalize

Let $w$ be the width of a perfect fifth interval, as a fraction of an octave. The value of $w$ depends on the tuning system.

• In Pythagorean tuning, $w = \log_2 \frac{3}{2} \approx 0.584963$
• In 12-ET, $w = \frac{7}{12} \approx 0.583333$.
• In 19-ET, $w = \frac{11}{19} \approx 0.578947$.
• In 31-ET, $w = \frac{18}{31} \approx 0.580645$.

More generally, a syntonic temperament allows $w \in [\frac{4}{7}, \frac{3}{5}] = [0.\overline{571428}, 0.6]$. In theory, you could define $w$ outside this range, but that would lead to weirdness like E being higher than F, flats being higher than sharps, or major intervals being wider than minor ones, so let's not do that.

Instead, let's define the Circle of Fifths distance of an interval $x$ (expressed as a fraction of an octave, so $x = \frac{s}{12}$) as the minimum distance to reach a frequency ratio with perfect fifths:

$$f(x) = \min \{ |n|: (nw - x) \in \mathbb{Z}, n \in \mathbb{Z}, \frac{4}{7} \le w \le \frac{3}{5} \}$$

Or, as an explicit piecewise function of $x$:

$$f(x) = \begin{cases} 0 && x = 0 \text{ or } x = 1\\ 1 && \frac{2}{5} \le x \le \frac{3}{7} \text{ or } \frac{4}{7} \le x \le \frac{3}{5} \\ 2 && \frac{1}{7} \le x \le \frac{1}{5} \text{ or } \frac{4}{5} \le x \le \frac{6}{7} \\ 3 && \frac{1}{5} < x \le \frac{2}{7} \text{ or } \frac{5}{7} \le x < \frac{4}{5} \\ 4 && \frac{2}{7} < x < \frac{2}{5} \text{ or } \frac{3}{5} < x < \frac{5}{7} \\ 5 && 0 < x < \frac{1}{7} \text{ or } \frac{6}{7} < x < 1 \\ 6 && \frac{3}{7} < x < \frac{4}{7} \end{cases}$$

Or, in terms of traditional interval nomenclature (with 12-ET semitones):

$$f(x) = \begin{cases} 0 && \text{P1 (0) or P8 (12)}\\ 1 && \text{P4 (5) or P5 (7)} \\ 2 && \text{M2 (2) or m7 (10)} \\ 3 && \text{m3 (3) or M6 (9)} \\ 4 && \text{M3 (4) or m6 (8)} \\ 5 && \text{m2 (1) or M7 (11)} \\ 6 && \text{A4 (6) or d5 (6)} \end{cases}$$

Note that under this revised formula, every interval has the same CoF distance as its octave inversion.