74

On a hot summer day like today, I like to put a six-pack of beer in my cooler and enjoy some cold ones outdoors.

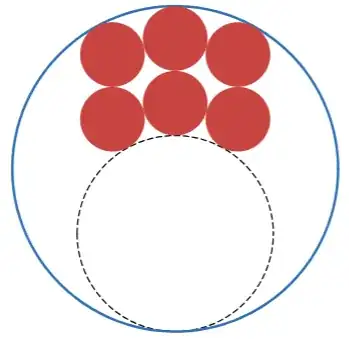
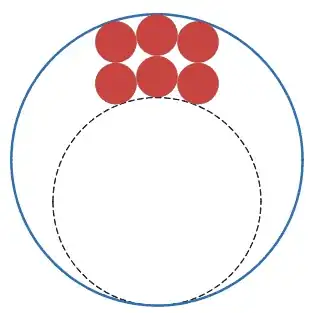
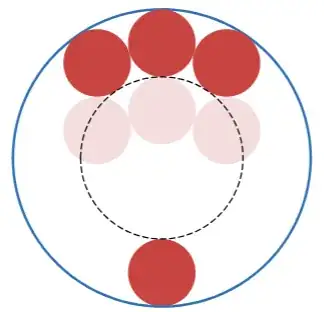
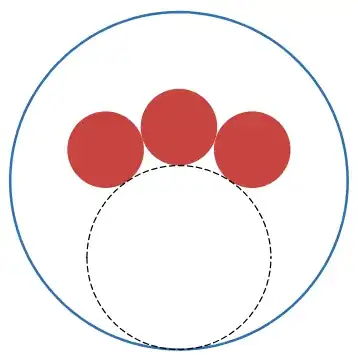
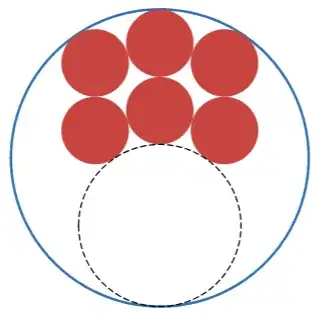
My cooler is in the shape of a cylinder. When I place the six-pack in the cooler against the wall, with three beer cans touching the wall, it seems that I can always draw an (imaginary) circle that is tangent to the other three beer cans and the opposite side of the wall, like this:

enter image description here

This seems to be true no matter what size the beer cans are (as long as they are the same size as each other).

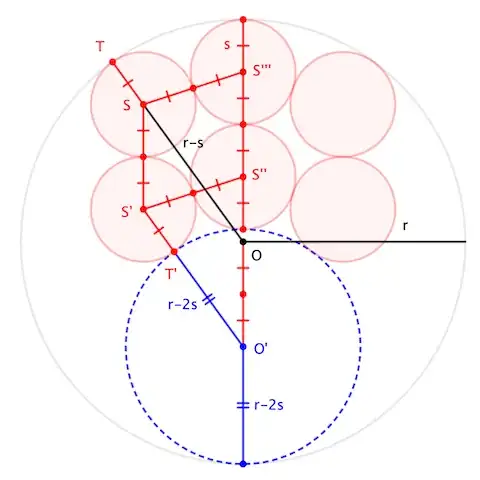
Is this true?

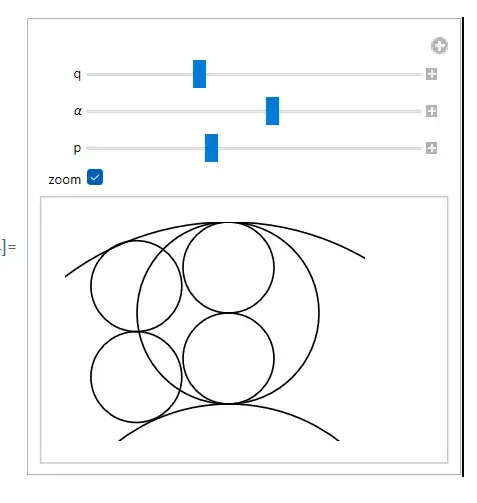
I made this animation:

enter image description here

Dan
  • 35,053

3 Answers3

50

Step 1

Remove the lower three beers from the six-pack. Put one of them at the bottom of the cooler. Obviously, we can draw a circle inside the cooler touching all four beers.

enter image description here

Step 2

Remove the bottom beer. Move the top three beers, and the circle, down, by a distance equal to the diameter of a beer.

enter image description here

Step 3

Put three beers back at the top.

enter image description here

Conclusion

The answer to the OP is: Yes.

It's not just six-packs

In the OP, if we replace "six-pack" with "$2n$-pack", the answer is still yes. In Step 1, instead of saying "Remove the lower three beers from the six-pack", say "Remove the lower $n$ beers from the $2n$-pack", etc.

Dan
  • 35,053
  • 3
    I just thought of this solution to my own question. I am surprised that my question had 700+ views and 25+ upvotes before someone posted this solution. – Dan Jul 01 '24 at 01:41
  • I think your first claim needs a bit of justification. Not every four points can be inscribed into a circle, even if we impose a reflection symmetry on them across the middle which is what I am guessing why you said it is obvious. – dezdichado Jul 01 '24 at 01:53
  • 2
    but I guess it is easy to prove that those four points are equidistant ($R-2r$) from the center of the large circle. – dezdichado Jul 01 '24 at 01:54
  • 1
    @dezdichado Slide a beer along the wall of the cooler. By symmetry, the envelope curve must be a circle. – Dan Jul 01 '24 at 01:59
  • 8
    I can't see how step 2 is obvious. If I start with 5 beers at the top in your step 1 for example, I can still shift all beers down as per step 2, but there wouldn't be enough space for 5 more beers after doing so. What makes 3 special? – hiccups Jul 01 '24 at 03:32
  • 2
    +1. Excellent. ... To @hiccups's point, there is a limitation to the can size in order for a second row of (however-many) cans to "physically" fit inside the cooler. That said, if we abandon the cans-and-cooler conceit, the idea of your argument shows generally that a "row" of circles (of diameter at most half that of the enclosing circle) can be translated in any direction by their diameter to obtain a second "row" that has a common tangent circle with the enclosing one. This, even though the rows may overlap each other or the boundary of the enclosure. – Blue Jul 01 '24 at 03:50
  • @hiccups I have edited to address your comment. If we replace "six-pack" with "$2n$-pack" (arranged as $2\times n$), the argument still works. – Dan Jul 02 '24 at 00:03
  • @Dan: There remains a can-size limitation in order for the translated row to fit inside the cooler. The resolution comes from your update to "Eight Circles": the initial row of $n$ cans must live within half of the bounding circle. The end-cans can be tangent to a diameter (as in Eight Circles), but a row crossing it will extend beyond the boundary after translation. (Again, this is only a problem for the physical cans-and-cooler story. In the abstract, the dashed circle exists even when the translated small circles overlap the boundary.) – Blue Jul 02 '24 at 00:56
  • 1
    @Blue My general solution assumes that the size of the cans is such that a $2n$-pack can fit in the cooler with half of the cans touching a wall. Then when we remove the lower row, and shift the upper row to the lower row's original position, then there will certainly be room for a new upper row. Incidentally, I worked out that in order for a $2n$-pack to fit in the cooler with half of the cans touching a wall, the radius of the cooler must be at least $\left(1+\csc\left[\frac{\pi}{6(n-2)}\right]\right)$ times a can's radius. – Dan Jul 02 '24 at 04:12
  • @Dan: True, there's certainly room for a new top row after translation; my point is that an initial row that doesn't fit into a semicircle will itself overlap the boundary after translation. ... Anyway ... It occurs to me, just now playing $n=5$, that there's another issue: past a certain size threshold (small radius about $0.15$-times boundary), cans in the lower row will overlap those in the upper row. (For $n=3$, the threshold ratio is $1/3$ (which we aren't "physically" allowed to pass), after which the lower-middle can overlaps the upper-left and -right cans.) – Blue Jul 02 '24 at 04:54
  • @Blue Yes, your "about $0.15$" is the reciprocal of my $\left(1+\csc\left[\frac{\pi}{6(n-2)}\right]\right)$ with $n=5$. – Dan Jul 02 '24 at 04:58
  • @Dan: Ah, okay. I didn't take from your comment that the formula had anything to do with preventing the rows of cans overlapping each other, so I didn't make the connection. – Blue Jul 02 '24 at 05:29
28

This one is fairly self-evident:

enter image description here

(Too-)Verbosely ... Let the enclosing circle have radius $r$ and center $O$. Let the small circles have radius $s$, and let the left-most four of these have centers (going counter-clockwise from top-left) $S$, $S'$, $S''$, $S'''$. Extend $OS$ to point of tangency $T$.

Now, note that $\square SS'S''S'''$ is a rhombus with sides $2s$. Let $O'$ complete parallelogram $\square SS'O'O$, so that $|OO'|=2s$, making $O'$ bisect the lower portion of the "vertical" diameter into lengths $r-2s$.

Also, $|O'S'|=|OS|=|OT|-|ST|=r-s$. Letting $O'S'$ meet $\bigcirc S'$ at $T'$, we conclude that $|O'T'|=|O'S'|-|S'T'|=r-2s$, the same distance as above. Consequently, $O'$ is the center of a circle with that radius, which is tangent to the lower three small circles (for any $s$ up to $r/3$), as suspected by OP.

(Of course, when $s=r/3$, we have a hexagonal cluster of seven equal circles within the enclosing one.)

Blue
  • 83,939
  • 1
    Is your point that due to symmetry we can remove the left or right hand beer can and then we just need to find a circle tangent to three others (middle can, side can, enclosing circle) which is https://en.wikipedia.org/wiki/Problem_of_Apollonius ? – Cong Chen Jun 30 '24 at 13:30
  • 3
    @CongChen: Interesting thought. However, as an Apollonian problem, there's no apparent reason for the circle tangent to middle-can, side-can, enclosing-circle to be tangent to the other side-can. The tangency properties among the cans and enclosure ultimately impose the desired symmetry. (They also threaten to over-determine the system and make a symmetry-respecting fourth circle impossible. That they don't over-determine the system is what makes the configuration interesting.) – Blue Jun 30 '24 at 14:50
  • 9
    Not self-evident at all, if you ask me! – TonyK Jun 30 '24 at 14:52
  • 1
    What tool was used to create this figure? – Jacob Ivanov Jun 30 '24 at 19:32
  • @JacobIvanov: I use GeoGebra (specifically, the GeoGebra Classic 5 desktop app) for my figures. – Blue Jun 30 '24 at 22:24
3

Not an answer, but the program to control the group of scaling and rotations

 Manipulate[
  Graphics[
   {Circle[],
    Circle[{0,-q},1-q],
    Circle[{0,1-q},q],
   tc={
      Circle[{0,1-q/2},q/2],
      Circle[{0,1-3q/2},q/2]},
   Rotate[Rotate[tc, -\[Alpha]  \[Pi], {0, p}], \[Alpha] \[Pi]]},
   PlotRange->If[zoom==1,{{-0.6,1/2},{0.2,1}},All]],
{{q,1/3},0,1},
{{\[Alpha],0.12},-1,1},
{{p,-0.26},-1,1},
{zoom,{0,1}} ]

4 packed circles between two tangent circles

Here the position of the circles is translated by a counter rotation around the origin following a rotation by $\alpha $ around a point $(0,p)$ on the y-axis.

The tangent conditions for $F(q,p,\alpha)=0$ have to be found, if possible.

Roland F
  • 5,122