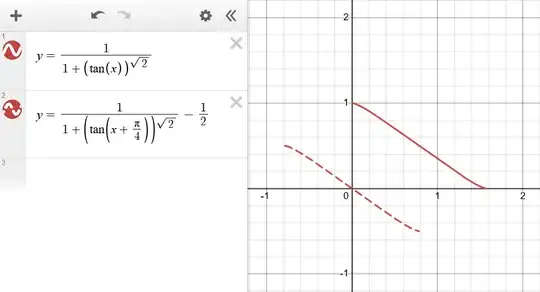
For example, Let us consider a function, say,
$f(x)=\frac{1}{1+tan^{\sqrt 2}x}$
This cannot be computed when it is indefinite. But, this can be integrated when we try to compute it with definite integration, using symmetry of this function.
Please refer this link for the graph and some explanation.
So my question now is, How do we say whether the graph of a given function is symmetrical or not. Is there any specific conditions under which the graph would be symmetrical?
Thanks in advance.
This is not a duplicate of the $\int\frac{1}{1+tan^{\alpha}x}dx$ question. This question is just used as an example.