You're given the ellipse $\frac{x^2}{a^2} + \frac{(y - b)^2}{b^2} = 1,$ for known $a$ and $b$. Now you slide the ellipse and rotate it such that it remains tangent to the $x$ axis at the origin all the time.
How can I compute the area of the region swept by the ellipse circumference as it slides and rotates. I think this has to do with envelopes, but I am not quite sure how to proceed.
Not a full answer, but I'm posting it in the hope it can be of help to find a complete solution.
We want to find the equation of an ellipse, with semi-axes $a$ and $b$, tangent to the $x$-axis at $(0,0)$, lying in the $y\ge0$ region and whose $a$ axis makes an angle $\theta$ with $x$-axis. We know that the general equation of an ellipse is $$ Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0 $$ and we can set:
$$ \begin{align} A&=a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta &B&=2\left(b^{2}-a^{2}\right)\sin \theta \cos \theta \\[1ex]C&=a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta &D&=-2Ax_{0}-By_{0 }\\[1ex]E&=-Bx_{0}-2Cy_{0}&F&=Ax_{0}^{2}+Bx_{0}y_{0}+Cy_{0}^{2}-a^{2}b^{2} \end{align} $$ where $(x_0,y_0)$ is the center of the ellipse.
Imposing that the ellipse is tangent to the $x$-axis at $(0,0)$ gives $F=0$ and $D=0$. This allows one to compute $(x_0,y_0)$ from the previous equalities (I chose the solution with $y_0\ge0$) and plug the result into $E$, obtaining: $$ E={B^2-4AC\over2\sqrt{A}}. $$ We can then write down the equation of the ellipse as: $$ \left(a^2 x^2+b^2 y^2\right)\sin^2t +\left(a^2 y^2+b^2 x^2\right)\cos^2t +\left(b^2-a^2\right) x y \sin2t -\frac{2 a^2 b^2 y}{\sqrt{a^2 \sin ^2t+b^2 \cos^2t}}=0. $$
To find the envelope of the ellipses as $\theta$ varies, one should eliminate $\theta$ between the above equation and its derivative with respect to $\theta$, but at the moment this looks quite difficult.
Here's the sliding ellipse obtained with GeoGebra, for $a=4$ and $b=2$:
And here's a figure of the envelope for the above ellipse:
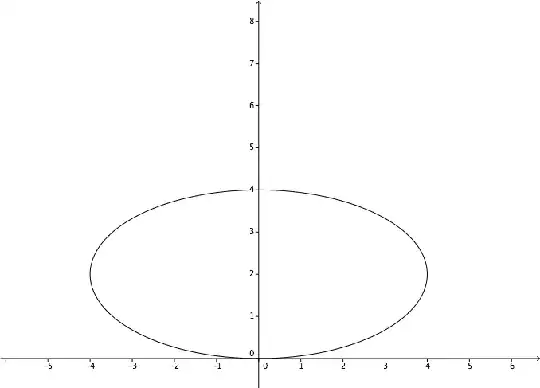
To find the sliding ellipse, using tangency properties, is quite easy.
Taking an ellipse as
$$ \mathscr{E}(x,y,x_0,y_0,a,b,t) = ((y-y_0)\cos t+(x-x_0)\sin t)^2a^2+((x-x_0)\cos t-(y-y_0)\sin t)^2-a^2b^2=0 $$
and the horizontal line
$$ \mathscr{L}(x,y)= y=0 $$
at tangency, eliminating $y$ we arrive at the polynomial
$$ p(x) = \sin ^2(t) \left(a^2 (x-x_0)^2+b^2 y_0^2\right)+\cos ^2(t) \left(a^2 y_0^2+b^2 (x-x_0)^2\right)-y_0 \sin (2 t) \left(a^2 x+b^2x_0\right)+a^2 x_0 y_0 \sin (2 t)+b^2 x y_0 \sin (2 t)-a^2 b^2=k (x-x_t)^2,\ \ \ \forall x $$
Note that at tangency, there is a double root ($(x-x_t)^2$), but we need that the tangent point be at the origin hence $x_t = 0$ and we have equivalently
$$ \left\{ \begin{array}{rcl} a^2 x_0^2 \sin ^2(t)+a^2 x_0 y_0 \sin (2 t)+a^2 y_0^2 \cos ^2(t)+b^2 x_0^2 \cos ^2(t)-b^2 x_0 y_0 \sin (2t)+b^2 y_0^2 \sin ^2(t)-a^2 b^2&=&0 \\ +b^2 y_0 \sin (2 t -2 a^2 x_0 \sin ^2(t)-a^2 y_0 \sin (2 t)-2 b^2 x_0 \cos ^2(t)&=&0 \\ a^2 \sin ^2(t)+b^2 \cos ^2(t)-k&=&0 \\ \end{array} \right. $$
Solving for $\{k,x_0,y_0\}$ we obtain
$$ \cases{ k = b^2\cos^2t+a^2\sin^2 t\\ x_0 = \pm\frac{\sqrt{2} (a^2-b^2) \sin (t) \cos (t)}{\sqrt{a^2+b^2-(a^2-b^2)\cos (2 t)}}\\ y_0 = \mp\frac{\sqrt{a^2+b^2-(a^2-b^2) \cos (2 t)}}{\sqrt{2}} } $$
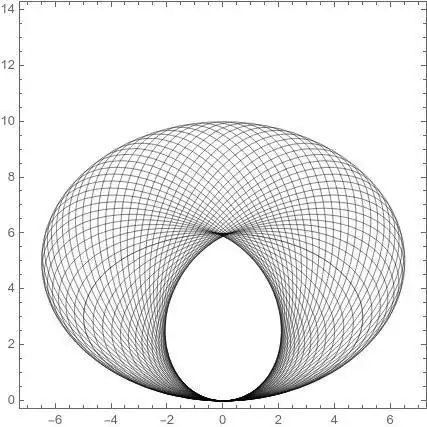
Now taking $\{a = 5, b = 3\}$ we have
NOTE
A precise numerical approximation can be obtained by following the steps.
1-Obtain the slipping ellipse equation, substituting $\{x_0(t), y_0(t)\}$ into $\mathscr{E}(x,y,x_0,y_0,a,b,t)$ giving $\mathscr{E}_s(x,y,a,b,t)$
2-Calculate $\dot{\mathscr{E}_s}(x,y,a,b,t)$
3-For $t = t_k, (k = 1,\cdots t_n)$ calculate $\{x_k,y_k\}$ as solutions for
$$ \cases{ \mathscr{E}_s(x,y,a,b,t_k) = 0\\ \dot{\mathscr{E}_s}(x,y,a,b,t_k)=0 } $$
now with the sequence $\{x_k,y_k\}$ we can interpolate a periodic spline obtaining an approximation as accurate as needed. Note that we can obtain independently the inner and outer points (in red).
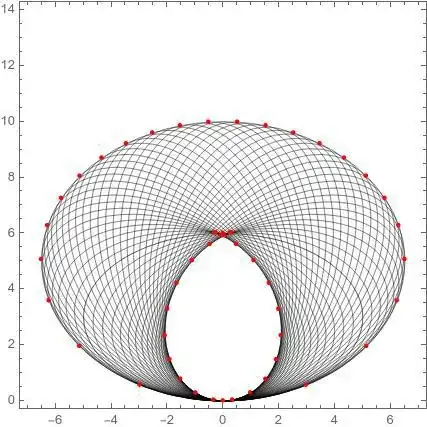
For this numerical case, the external area as depicted in the following picture in light blue, is approximately $101.90783$ units.
Regarding the inner points, we have a region as can be depicted in the following picture, with an approximate area of $18.2331$ units.
