Mean Angle to Points on a Cone

Question

Consider a cone of radius $r$ and height $h$. Define $m=\frac{h}{r}$. Its equation is given below.

\begin{align} z(x,y)=-m\sqrt{x^2+y^2}+h\hspace{5mm}z\geqslant0 \end{align}

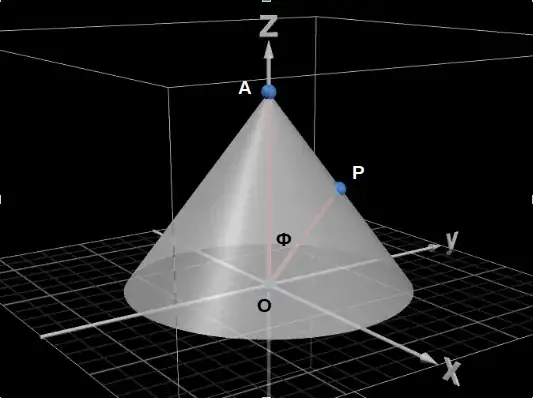
Let $O$ represent the center of the cone's base (the origin).

Let $A$ represent the apex of the cone $(0,0,h)$.

Let $P_j$ represent an arbitrary point on the cone.

Define $\phi_j$ as $\angle AOP_j$.

What is the mean value of $\phi_j$ assuming a uniform distribution of points across the manifold?

I believe the answer may be $\frac{\pi}{2}-\arctan\left(\frac{h}{2r}\right)$.

My approach:

Let's define $\bar \phi$ as the average value of $\phi_j$. It can be calculated as shown below:

\begin{align} \bar \phi&=\cfrac{\int\limits_0^{\pi/2}\cfrac{\phi d\phi}{\tan\phi+m}}{\int\limits_0^{\pi/2}\cfrac{d\phi}{\tan\phi+m}} \end{align}

We'll break this up into the following two integrals:

\begin{align} I_1&=\int\limits_0^{\pi/2}\cfrac{\phi d\phi}{\tan\phi+m} \\ I_2&=\int\limits_0^{\pi/2}\cfrac{d\phi}{\tan\phi+m} \end{align}

These are two very challenging integrals. I have solved $I_2$, as shown below. However, I have not been able to solve $I_1$.

Solution for $I_2$

\begin{align} I_2&=\int\limits_0^{\pi/2}\cfrac{d\phi}{\tan\phi+m} \end{align}

First, we'll multiply the integrand by $\frac{\sec^2\phi}{1+\tan^2\phi}$.

\begin{align}I_2&=\int\limits_0^{\pi/2}\cfrac{\sec^2\phi d\phi}{(\tan\phi+m)(1+\tan^2\phi)} \end{align}

Next, we'll substitute.

\begin{align} u&=\tan\phi \\ du&=\sec^2\phi d\phi \\ [0,\pi/2)&\mapsto[0,\infty) \\ \\ \implies I_2=\int\limits_0^\infty\frac{du}{(u+m)(u^2+1)} \end{align}

Now we must do a partial fraction decomposition.

\begin{align} \frac{A}{u+m}+\frac{Bu+C}{u^2+1}&=\frac{1}{(u+m)(u^2+1)} \\ A(u^2+1)+(Bu+C)(u+m)&=1 \\ \end{align}

Case 1: $u=-m$

\begin{align} A(m^2+1)&=1 \\ A&=\frac{1}{m^2+1} \end{align}

Case 2: $u=0$

\begin{align} A+Cm&=1 \\ \frac{1}{m^2+1}+Cm&=1 \\ Cm&=\frac{m^2+1}{m^2+1}-\frac{1}{m^2+1} \\ C&=\frac{m}{m^2+1} \end{align}

Case 3: $u=-2m$

\begin{align} A(4m^2+1)+(-2B+C)(-m)&=1 \\ \frac{4m^2+1}{m^2+1}+2Bm^2-\frac{m^2}{m^2+1}&=1 \\ 2Bm^2+\frac{3m^2+1}{m^2+1}&=1 \\ 2Bm^2&=\frac{m^2+1}{m^2+1}-\frac{3m^2+1}{m^2+1} \\ B&=-\frac{1}{m^2+1} \end{align}

Let $k=\frac{1}{m^2+1}$, then rewrite the coefficients.

\begin{align} A&=k \\ B&=-k \\ C&=km \end{align}

Rewriting $I_2$ accordingly,

\begin{align} I_2&=\int\limits_0^\infty\frac{k}{u+m}-\frac{ku-km}{u^2+1} du \\ I_2&=\lim_{n\to\infty}k\ln|u+m|\bigg\rvert_0^n-\frac{k}{2}\int\limits_0^\infty\frac{2u}{u^2+1} du+km\int\limits_0^\infty\frac{du}{u^2+1} \\ I_2&=\lim_{n\to\infty}\left[k\ln|u+m|\bigg\rvert_0^n-\frac{k}{2}\ln|u^2+1|\bigg\rvert_0^n+km\arctan(u)\bigg\rvert_0^n\right] \\ \end{align}

To match the coefficients of the first two valuations, note $\ln|x|=\frac{1}{2}\ln x^2$.

\begin{align} I_2&=\lim_{n\to\infty}\left[\frac{k}{2}\left(\ln(u+m)^2-\ln(u^2+1)\right)\bigg\rvert_0^n+\frac{km\pi}{2}\right] \\ I_2&=\frac{k}{2}\lim_{n\to\infty}\left[\ln\left(\frac{u^2+2mu+m^2}{u^2+1}\right)\bigg\rvert_0^n+m\pi\right] \\ I_2&=\frac{k}{2}\left(m\pi-2\ln|m|\right) \end{align}

Substituting $k=\frac{1}{m^2+1}$,

\begin{align} I_2&=\frac{m\pi-2\ln|m|}{2(m^2+1)} \end{align}

Substituting $m=\frac{h}{r}$,

\begin{align} I_2&=\frac{\frac{\pi h}{r}-2\ln\left|\frac{h}{r}\right|}{\left(\frac{h}{r}\right)^2+1} \\ I_2&=\cfrac{\pi rh+2r^2\ln\left(\frac{h}{r}\right)}{2(r^2+h^2)} \end{align}

My Question

I believe $I_1$ is only solvable through nonelementary methods--I have tried integrating by parts but the resulting integrand looks daunting. I would like a solution to that integral OR a different approach to solving the problem.

Thank you.

Answer 1

We start with the easier one. $$ \begin{aligned} I_2&=\int_0^{\frac{\pi}{2}} \frac{\cos \phi}{\sin \phi+m \cos \phi} d \phi\\&= \int_0^{\frac{\pi}{2}} \frac{\frac{m}{1+m^2}(\sin \phi+m \cos\phi)+\frac{1}{1+m^2}(\cos \phi-m \sin \phi)}{\sin \phi+m \cos \phi} d \phi\\& =\frac{1}{1+m^2}\left(m \int_0^{\frac{\pi}{2}} d \phi+\int_0^{\frac{\pi}{2}} \frac{d(\sin \phi+m \cos \phi)}{\sin \phi+m \cos \phi} \right) \\ &=\frac{1}{1+m^2}\left(\frac{m \pi}{2}+ \left[\ln |\sin \phi+m \cos \phi|\right]_0^{\frac{\pi}{2}}\right) \\ & =\frac{1}{1+m^2}\left(\frac{m \pi}{2}-\ln m\right) \\ & \end{aligned} $$

---

Let’s investigate the harder one. Using the same trick used in $I_2$ above, we have $$ \begin{aligned} I_1 & =\frac{1}{1+m^2}\left[\frac{m \pi^2}{8}+\int_0^{\frac{\pi}{2}} \phi \,d(\ln (\sin \phi+m \cos \phi))\right] \\ & =\frac{1}{1+m^2}\left[\frac{m \pi^2}{8}- \underbrace{\int_0^{\frac{\pi}{2}} \ln (\sin \phi+m \cos \phi) d \phi}_{J(m)} \right] \quad \textrm{ (via IBP)} \end{aligned} $$

Now Use Feynman’s trick by differentiating $I(m)$ w.r.t.$m$ $$ \begin{aligned} J^{\prime}(m) & =\int_0^{\frac{\pi}{2}} \frac{\cos \phi}{\sin \phi+m \cos \phi} d \phi \\&=I_2\\ & =\frac{1}{1+m^2}\left(\frac{m \pi}{2}-\ln m\right) \end{aligned} $$ Integrating back from $x=0$ to $ m $ yields

$$ J(m)-J(0)=\int_0^m J^{\prime}(x) d x=\int_0^m \frac{1}{1+x^2}\left(\frac{\pi x}{2}-\ln x\right) d x $$ Using the fact that $J(0)=-\frac{\pi}{2}\ln 2$, we get $$ \begin{aligned}J(m)&=\frac{\pi}{2} \ln 2+ \underbrace{\frac{\pi}{2} \int_0^m \frac{x}{1+x^2} d x}_{=\frac \pi {4}\ln(1+m^2)} -\int_0^m \frac{\ln x}{1+x^2} d x\\&= \frac{\pi}{2} \ln 2+\frac{\pi}{4} \ln \left(1+m^2\right)- \left[\ln m \tan ^{-1} m-\frac{i}{2} \operatorname{L i_2}(-i m)+\frac{i}{2} \operatorname{L i_2}(i m)\right] \end{aligned}$$ (For details of the last integral, please see the footnote below.)

Hence we can conclude that $$ \boxed{I_1=\frac{1}{1+m^2}\left[\frac{m \pi^2}{8}-\frac{\pi}{2} \ln 2-\frac{\pi}{4} \ln \left(1+m^2\right) +\ln m \tan ^{-1} m -\frac{i}{2} \operatorname{L i_2}(-i m)+\frac{i}{2} \operatorname{L i_2}(i m) \right]} $$

---

Footnote:

Noting that $$\begin{aligned} \frac{1}{1+x^2} & =\frac{1}{2 i}\left(\frac{1}{i+x}+\frac{1}{i-x}\right) \\ \Rightarrow \tan ^{-1} x & =\frac{1}{2 i} \ln \left(\frac{i+x}{i-x}\right)=\frac{1}{2 i} \ln \left(\frac{1+\frac{x}{i}}{1-\frac{x}{i}}\right)\end{aligned}$$ and using integration by parts, we have $$ \begin{aligned} \int_0^m \frac{\ln x}{1+x^2} d x&=\ln m \tan ^{-1} m-\int_0^m \frac{\tan ^{-1} x}{x} d x \\ & =\ln m \tan ^{-1} m+\frac{i}{2} \int_0^m\left[\frac{\ln \left(1+\frac{x}{i}\right)}{x}-\frac{\ln \left(1-\frac{x}{i}\right)}{x}\right] d x \\ & =\ln m \tan ^{-1} m-\frac{i}{2} \operatorname{Li_2}(-im)+\frac{i}{2} \operatorname{Li_2}(im) \end{aligned} $$

Answer 2

You suspect correctly that $I_1$ is non-elementary. Integrate by parts and denote the subsequent integral by $J(m)$,

$$I_1 = \int_0^\tfrac\pi2 \frac{\phi}{\tan\phi+m} \, d\phi = -\frac{1}{1+m^2} \underbrace{\int_0^\tfrac\pi2 \log(\sin\phi + m \cos\phi) \, d\phi}_{J(m)}$$

Differentiate w.r.t. $m$ and evaluate the $\phi$-integral; this can be done with the famous tangent half-angle substitution and partial fraction decomposition.

$$\begin{align*} J'(m) &= \int_0^\tfrac\pi2 \frac{\cos\phi}{\sin\phi+m\cos\phi} \, d\phi \\ &= 2 \int_0^1 \frac{1-t^2}{\left(1+t^2\right) \left(m+2t-mt^2\right)} \, dt \\ &= \frac{\frac{m\pi}2 - \log m}{1+m^2} \\ \end{align*}$$

Together with the well-known value of

$$J(0)=\displaystyle\int_0^\tfrac\pi2\log(\sin\phi)\,d\phi=-\frac\pi2\log2,$$

we can use the fundamental theorem of calculus to attempt to recover $J(m)$ :

$$\begin{align*} J(m) &= J(0) + \int_0^m \frac{\frac{\mu\pi}2 - \log \mu}{1+\mu^2} \, d\mu \\ &= -\frac\pi4 \log2 - \int_0^m \frac{\log\mu}{1+\mu^2} \, d\mu \end{align*}$$

The last integral can be evaluated in terms of dilogarithms of complex argument; see a similar antiderivative found here.