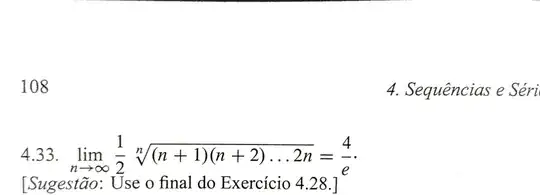An analysis question about limits and sequences

Asked Jun 25 '24 at 09:23

Active Jun 25 '24 at 09:43

Viewed 48 times

I'm having a hard time proving:

$\lim_{n\to\infty} \frac{1}{2} \sqrt[n]{(n+1)(n+2)...(2n)}= \frac{4}{e}$

any tips?

The book I found this exercise in says I should use the following property: If a sequence $a_n$ has only strictly positive terms and $\lim_{n\to\infty} \frac{a_{n+1}}{a_n}=a$, then $\lim_{n\to\infty} \sqrt[n]{a_n}=a$

edited Jun 25 '24 at 09:43

asked Jun 25 '24 at 09:23

Igor Paulino

1

Check https://math.stackexchange.com/q/99324/42969 and the linked questions. – Martin R Jun 25 '24 at 09:32
1

The first factor $1/2$ should probably be $1/n$. – Martin R Jun 25 '24 at 09:32
Yes, it seems the book got it wrong, thank you for the help – Igor Paulino Jun 25 '24 at 09:38
1

A search with Approach0 shows that this has been asked and answered several times – Martin R Jun 25 '24 at 09:39
Well, in my defense, the book has stated the problem, not me, I'll add a photo – Igor Paulino Jun 25 '24 at 09:41
But I found this tool approach0 very useful, I intend to use it in the future, thank you very much – Igor Paulino Jun 25 '24 at 09:46
1

I am voting to close this post as a(n erroneous) duplicate of How to prove that $\lim \frac{1}{n} \sqrt[n]{(n+1)(n+2)... 2n} = \frac{4}{e}$ – Anne Bauval Jun 25 '24 at 09:47

An analysis question about limits and sequences

0 Answers0