Find the angle $ECA$

Question

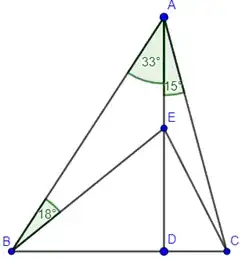
I found this puzzle some time ago on the Internet. Triangle $ABC$ is like on the picture:

where $AD$ is an altitude. One need to find angle $ECA$. How to solve it?

Insane attempt:

1. $\left|\angle EBD\right|=39^\circ, \left|\angle DEB\right|=51^\circ$
2. Set $\left|AB\right|=1, \left|\angle ECA\right|=\alpha$
3. $\left|BD\right|=\sin{33^\circ}, \left|AD\right|=\cos{33^\circ}$
4. $\left|ED\right|=\sin{33^\circ}\cdot \tan{39^\circ}$
5. $\left|DC\right|=\cos{33^\circ}\cdot \tan{15^\circ}$
6. $\tan{\left(75^\circ-\alpha\right)}=\frac{\sin{33^\circ}\cdot\tan{39^\circ}}{\cos{33^\circ}\cdot\tan{15^\circ}}=\frac{\tan{33^\circ}\cdot\tan{39^\circ}}{\tan{15^\circ}}$
7. $\alpha=75^\circ-\tan^{-1}{\left( \frac{\tan{33^\circ}\cdot\tan{39^\circ}}{\tan{15^\circ}} \right)}$
8. After proving (I wasn't able to) that $\tan{33^\circ}\cdot\tan{39^\circ} = \tan{15^\circ}\cdot\tan{63^\circ}$ we are getting $\alpha=12^\circ$

Alternative question would be: How to prove $\tan{33^\circ}\cdot\tan{39^\circ} = \tan{15^\circ}\cdot\tan{63^\circ}$?

Answer 1

Here is an answer to what you call "the alternative question" :

$$\tan{33^\circ}\cdot\tan{39^\circ} = \tan{15^\circ}\cdot\tan{63^\circ} \ ? \ \ \tag{1}$$

that we write under the form :

$$\frac{\tan{33^\circ}}{\tan{15^\circ}}=\frac{\tan{63^\circ}}{\tan{39^\circ}} \ ? \ \ \tag{1'}$$

---

Let us first establish that the LHS of (1') can be written under the form :

$$\frac{\tan 33°}{\tan 15°}=\frac{\tan 21°}{\tan 9°}\tag{2}$$

which is equivalent to :

$$\tan 21° \tan 15° = \tan 33° \tan 9° \tag{2'}$$

An identity which is given and proved here

Let us copy the first part of their proof : (2) can be transformed into :

$$\underbrace{\sin 33° \cos 15°}\underbrace{ \sin 9° \cos 21°} =\underbrace{ \sin 15° \cos 33° }\underbrace{\sin 21° \cos 9°}$$

which can be transformed, using classical formulas into :

$$\frac 12 (\sin 48°+\sin 18°) \frac 12 (\sin 30°-\sin 12°)=\frac 12 (\sin 48° -\sin 18°)\frac 12 (\sin 30° +\sin 12°)$$

giving :

$$\sin 18° \sin 30° = \sin 48° \sin 12°$$

$$\sin 18° = 2 \sin 48° \sin 12°$$

$$\cos 72° = \cos 36° - \cos 60°$$

which is true by using exact formulas that can be found there.

---

Besides, let us establish that the RHS of (1') can be written under the form :

$$\frac{\tan{63^\circ}}{\tan{39^\circ}}=\frac{\tan{21^\circ}}{\tan{9^\circ}} \tag{3}$$

For this purpose, we apply the following identity (that can be found with proof here) :

$$\tan(3x)=\tan x . \tan (60°-x) . \tan (60°+x)$$

to the case $x=21°$ :

$$\tan 63° = \tan 21° \tan 39° \tan 81°$$

which is equivalent to :

$$\tan 63° \tan 9° = \tan 21° \tan 39°$$

proving (3).

Comparison of (2) and (3) gives (1').

Answer 2

We have $\tan(33)=\frac{BD}{AD}$ and $\tan(15)=\frac{CD}{AD}$, so $\frac{\tan(33)}{\tan(15)}=\frac{BD}{CD}$.

But also, $\tan(51)=\frac{BD}{ED}$ and $\tan(DEC)=\frac{CD}{ED}$, so $\frac{\tan(51)}{\tan(DEC)}=\frac{BD}{CD}$.

Can you get it from here? (If you get angle DEC, you can get DCE and thus ECA.)

Answer 3

The question can be put in more general terms. Are there triangles which can be dissected in four subtriangles, connected in point E on the altitude. The given triangle is just one example. And proving that indeed the product of these tangents is equal on both sides is not trivial. I did a numercial search and found many of these triangles. Just one example.. Again, proving is not trivial.