3

Solve irrational equation: $$(2x-7)(\sqrt {3x-2}-\sqrt {x+3})=5$$ I tried multiplying everything out and using conjugates, but it became too lengthy. As a result, I only obtained one solution $x=1$, and the remaining equation was too complex for me to solve. $$2(x\sqrt{3x-2}-1)-2(x\sqrt{x+3}-2)-7(\sqrt{3x-2}-1)+7(\sqrt{x+3}-2)=0$$.
Could you please help me solve this problem? Thank you!

Felix Marin
  • 94,079
SpyroK
  • 41
  • 3
  • Where did this problem come from, please? – Gerry Myerson Jun 14 '24 at 12:28
  • When you square the thing, you only have one root left. What do you need to do in order to get rid of that root? – Dominique Jun 14 '24 at 12:30
  • 2
    You can plot it to confirm that there are exactly two solutions, and then remark that there are two "obvious" integral solutions. To be sure, this line of attack depends on being confident that the solutions will be pleasant. For instance, the same reasoning fails if you replace $5$ by $4$ or $6$. – lulu Jun 14 '24 at 12:31
  • 2
    There is no diffrential equations anywhere, why have you tagged your question "ordinary-differential-equations". – Henrik supports the community Jun 14 '24 at 12:32
  • @GerryMyerson It comes from a test in my city – SpyroK Jun 14 '24 at 12:39
  • Are you supposed to ask people to help you on this test? – Gerry Myerson Jun 14 '24 at 12:40
  • @Henriksupportsthecommunity I'm sorry, but I don't understand why switching tags causes an error – SpyroK Jun 14 '24 at 12:40
  • @GerryMyerson I'm just practicing test papers to prepare for exams, so I want to explore new ideas. With everyone's help, there's nothing better. – SpyroK Jun 14 '24 at 12:44
  • Square it, re-arrange it, square it again. Factorize and check the solutions solve the original equation. – Paul Jun 14 '24 at 13:06
  • get a piece of graph paper, plot some points and draw two things, $y = \sqrt{3x-2} - \sqrt{x+3},$ which resembles half a parabola. Then $y = \frac{5}{2x-7} ,$ which is a hyperbola. Becomes clear there are two (real) intersections. – Will Jagy Jun 14 '24 at 15:56
  • You could square it, isolate the square root, and square again, but that gives you an ugly 6th-degree polynomial. Though, it does have two integer roots (1 and 6). – Dan Jun 14 '24 at 17:00
  • Using Sage to eliminate for $x$ in the system $(2x-7)(y-z)=5, y^2=3x-2, z^2=x+3$, I get a result of $(x-6)(x-1)(16x^4-192x^3+956x^2-2380x+2425) = 0$. (Of course, that could introduce extraneous roots since it doesn't apply the restrictions $y \ge 0, z \ge 0$. The quartic factor appears to have two real roots near 3 and 4, which I guess will indeed end up being extraneous solutions.) – Daniel Schepler Jun 14 '24 at 18:37

3 Answers3

1

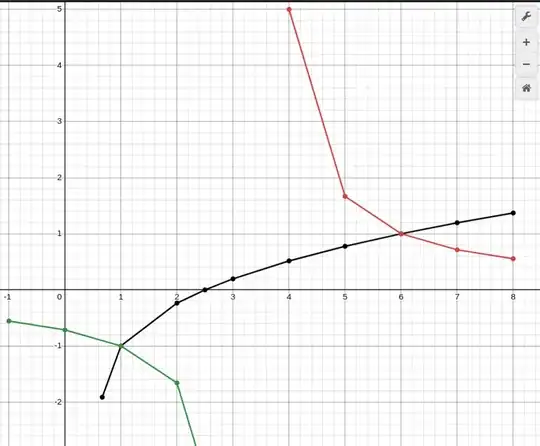
as I commented, drawing a picture, by plotting points yourself, is a good way to find out what to expect. Together, the red and green curves make up a hyperbola, that is the $y = \frac{5}{2x-7}.$ The black curve, resembling half a parabola, is the bit with the square roots, $y = \sqrt{3x-2} -\sqrt{x+3}$. Two intersections. Oh, it became clear that the black curve met the $x$ axis at $\frac{5}{2}$

enter image description here

Finally managed to solve for $x$ in the square root thing, $$ x = \frac{1}{8} \, \left( \, 20 + 8 y^2 + y \sqrt{48y^2 + 352} \; \right) $$ Got this by squaring, this one allows for arbitrary real $y$

Will Jagy
  • 146,052
1

By algebra, $$(2x-5)^2(2x-7)^4-50(4x+1)(2x-7)^2+625=0.$$ Here is the trick: $2x-7=u.$ Then by polynomial division, $$(u+5)(u-5)(u^4+4u^3+29u^2-25)=0.$$ The easy roots $u=\pm5$ give $x=1,6$.

Bob Dobbs
  • 15,712
1

Squaring the equation gives:

$$(2x-7)^2(\sqrt{3x-2}-\sqrt{x+3})^2=25$$ $$(2x-7)^2((3x-2) - 2\sqrt{(3x-2)(x+3)} + (x+3))=25$$ $$(2x-7)^2\left( 4x + 1 - 2\sqrt{3x^2+7x-6} \right) = 25$$

Isolating the square root gives:

$$\sqrt{3x^2+7x-6} = \frac{\frac{25}{(2x-7)^2} - 4x - 1}{-2}$$ $$\sqrt{3x^2+7x-6} = \frac{8x^3 - 54x^2 + 84x + 12}{4x^2 - 28x + 49}$$

Squaring again gives:

$$3x^2+7x-6 = \frac{(8x^3 - 54x^2 + 84x + 12)^2}{(4x^2 - 28x + 49)^2}$$ $$(3x^2+7x-6)(4x^2 - 28x + 49)^2 - (8x^3 - 54x^2 + 84x + 12)^2 = 0$$

Fully expanding this polynomial (I'm going to skip a few steps here) gives:

$$-16 x^6 + 304 x^5 - 2396 x^4 + 10224 x^3 - 24821 x^2 + 31255 x - 14550 = 0$$

Testing some small-integer candidate roots gives $x = 1$ and $x = 6$ as potential solutions. Factoring out $x - 1$ and $x - 6$ gives:

$$-(x - 1) (x - 6) (16 x^4 - 192 x^3 + 956 x^2 - 2380 x + 2425) = 0$$

It's possible to find closed-form solutions for a quartic, but it involves a crazy mess of radicals, so I won't even bother. So instead, here are numerical approximations of the roots:

$$x \approx 3.010093734458125$$ $$x \approx 3.933735131749346$$ $$x \approx 2.5280855668962645 \pm 2.531538034879342i$$

Solving the quartic turns out to be useless anyway, since neither of the irrational roots is a solution of the original equation, but are extraneous solutions introduced by squaring.

>>> def f(x):
...     return (2 * x - 7) * (math.sqrt(3 * x - 2) - math.sqrt(x + 3))
...
>>> f(1)
5.0
>>> f(6)
5.0
>>> f(3.010093734458125)
-0.1958826448520943
>>> f(3.933735131749346)
0.4315569460231007

So, assuming that you don't care about complex numbers, $\boxed{x \in \{1, 6\}}$.

Dan
  • 18,262