10

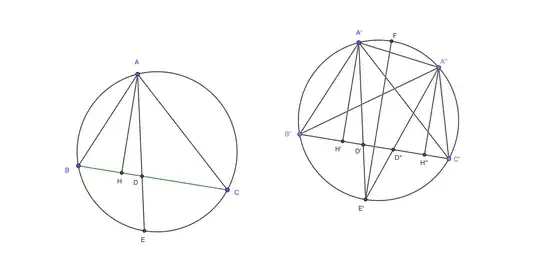
Given $\Delta ABC, \Delta A'B'C'$ s.t $\widehat{BAC}=\widehat{B'A'C'}, BC=B'C', AD=A'D'$ $(AD, A'D'$ are internal bisectors of $\widehat{BAC}, \widehat{B'A'C'}$ respectively).

Prove that $\Delta ABC=\Delta A'B'C'$.

My attempt:
Let $E\in\vec{AB}, F\in\vec{AC}$ s.t $AE=A'B', AF=A'C'$. Then $\Delta AEF=\Delta A'B'C'\Rightarrow EF=B'C'$.
On the other hand $\Delta AED=\Delta A'B'D'\Rightarrow ED=B'D'$. Similarly, $DF=D'C'$.
So, $ED+DF=B'D'+D'C'=B'C'=EF\Rightarrow E,D,F$ are collinear and $D$ is between $E,F$.
I'm stuck here :( . Could someone help me? Here's a picture: enter image description here Thanks in advance.

math-physicist
  • 1,294
Harry
  • 101
  • Construct a replica of $A'B'C'$, say $A''B''C''$, such that $C''\equiv B$ and $B'' \equiv C$. $ABC$ and $A''B''C''$ share the same circumcircle $\gamma$. Let $A''D''$ the internal bisector of $\angle B''A''C''$. Extended $AD$ to $E\in \gamma$ and $A''D''$ to $E''\in \gamma$. Since $BE\cong BE''$ (the subtend congruent angles on $\gamma$) it must be $E\equiv E''$... – dfnu Jun 08 '24 at 08:18
  • @dfnu how to make sure that there exists such $\Delta A''B''C''$? – lee max Jun 08 '24 at 08:37
  • @leemax If I understand the question correctly, the existence is guaranteed by the fact that $BC \cong B'C'$. There are actually two triangles. I meant the one on the same half-plane where $A$ lies, wrt $BC$. – dfnu Jun 08 '24 at 08:44
  • @dfnu how you continue? – lee max Jun 08 '24 at 10:13
  • Are you allowed to use the angle bisector theorem? – Intelligenti pauca Jun 08 '24 at 10:44
  • @Intelligentipauca I suppose yes – Harry Jun 08 '24 at 11:03
  • @leemax I just wanted to give a hint to OP, otherwise I would have posted an answer. – dfnu Jun 08 '24 at 11:45
  • @dfnu could you show the rest of the problem? I still don't know how to continue :( – Harry Jun 08 '24 at 11:59

2 Answers2

3

Take chord BC as a fixed line segment. Then all the possible positions of A lie on a circle through B and C (as BAC is fixed). The angle bisector at A then always passes through the point P which is the midpoint of the arc BC not containing A (equal angles subtend equal arcs at the circumference). Let D be the point of intersection of AP and BC. Then the length of the bisector, AD, equals AP less DP.

First consider A to be diametrically opposite P. Then as A is moved round the circle towards P, distance AP decreases and the distance PD increases, so the length of the bisector decreases. Hence there will only be one triangle with the desired bisector length.

mcd
  • 4,231
2

This is an attempt at indirect proof.

Since $BC=B’C’$ and the angles at $A$, $A’$ are equal, the triangles’ vertices lie on equal circles, and angle bisectors $AD$, $A’D’$ extended bisect the arcs below the triangle bases at $E$, $E’$.

Given that $AD=A'D'$, suppose $\triangle ABC\ne\triangle A’B’C’$.

Since their bases are equal, then their heights must be unequal. ABC=A'B'C' Supposing height $A’H’>AH$, and constructing $A’’H’’ =AH$, then $\triangle A''B'C'=\triangle ABC$.

Drawing $E’F\perp B’C’$, $E’F$ is a diameter, and we know $A'A'' \nparallel B’C’$.

Since here $E’A’’<E’A’$ (Euclid, Elements, III, 7), while $E’D’’>E’D’$, then remainder$$ A’’D’’<A’D’=AD$$and $\triangle A''B'C'$ does not fulfill the given conditions.

And the same result follows if we suppose height $A’H’<AH$.

Therefore, if $\angle BAC=\angle B'A'C'$, and $BC=B'C'$, and angle bisector $AD=A'D'$, then $$\triangle ABC=\triangle A'B'C'$$

Edward Porcella
  • 5,178