How to find a point within a triangle from perpendiculars taken from the edges

Question

Given a point on each edge of the triangle, where, if you were to take the perpendicular of the edge from that point, all 3 perpendiculars would intersect a single point, how could I find the position of that single intersection point, given the positions of the points and the vertices of the triangle.

I am not looking for the orthocenter, in my context the points may lie anywhere on the triangle’s edges and not just at the middle of them, even though the first two constrict the third. I am looking for a general formula to finding the intersection, efficiently (essentially have as little operations as possible through any way you can think of).

Answer 1

Consider $\triangle ABC$ with perpendiculars at points $D$, $E$, $F$ on the side-lines meeting at point $P$, as shown:

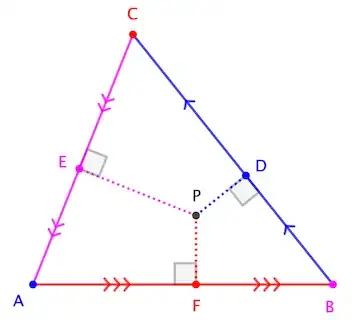
The positions of $D$, $E$, $F$ are not independent; choosing any two constrains the third. The Ceva-like relation governing these positions is known as Carnot's Theorem:

$$|DC|^2+|EA|^2+|FB|^2 \;=\; |BD|^2+|CE|^2+|AF|^2 \tag1$$ Equivalently, since $a=|DC|+|BD|$, etc, we find $$a\,|DC| + b\,|EA| + c\,|FB| \;=\; a\,|BD| + b\,|CE| + c\,|AF| \tag2$$

(A decade(!) ago, I (re-)proved this theorem in this Math.SE answer. I dubbed the result "Ortha's Theorem" as a back-construction of "orthian", a term I coined for the perpendiculars at $D$, $E$, $F$, mimicking the name "cevian" and its derivation from Ceva's Theorem.)

With a little bit of effort, and some manipulation based on $(1)$ or $(2)$, one can derive the following barycentric representation of the point $P$:

$$P = \frac{u A + v B + w C}{u+v+w}$$ where $$\begin{align} u &\;:=\; a\;\left(\; -a\,|BD||DC| \;+\;b\,|BD||CE| \;+\;c\,|FB||DC| \;\right) \tag3 \\[4pt] v &\;:=\; b\;\left(\; -b\,|CE||EA| \;+\;c\,|CE||AF| \;+\;a\,|DC||EA| \;\right) \tag4 \\[4pt] w &\;:=\; c\;\left(\; -c\,|AF||FB| \;+\;a\,|AF||BD| \;+\;b\,|EA||FB| \;\right) \tag5 \\[4pt] u+v+w &\;=\; 4\,|\triangle ABC|^2 \tag6 \end{align}$$

In the above, $|\triangle ABC|$ represents the area of the triangle. Also, distances are considered "signed" relative to the oriented sides $\overrightarrow{AB}$, $\overrightarrow{BC}$, $\overrightarrow{CA}$ of the triangle. For instance, $|AF|$ is positive when $\overrightarrow{AF}$ and $\overrightarrow{AB}$ point in the same direction; and negative when in the opposite direction.

• When $D$, $E$, $F$ are midpoints, so that $$|BD|=|DC|=\tfrac12a \qquad |CE|=|EA|=\tfrac12b \qquad |AF|=|FB|=\tfrac12c$$ then $$u:v:w \;=\; a \cos A : b \cos B : c \cos C \tag7$$ These are the barycentric coordinates of the circumcenter.

• When $D$, $E$, $F$ are the feet of altitudes, so that $$|BD|=c\cos B \qquad |DC|=b\cos C \qquad \text{etc}$$ then $$u:v:w \;=\; \frac{a}{\cos A}:\frac{b}{\cos B}:\frac{c}{\cos C} \tag8$$ These are the barycentric coordinates of the orthocenter.

• When $D$, $E$, $F$ are the "touch points" of the incircle, so that $$\begin{align} |EA|=|AF|&=\tfrac12(-a + b + c) \\ |BD|=|FB|&=\tfrac12(-b + c + a) \\ |DC|=|CE|&=\tfrac12(-c + a + b) \end{align}$$ then $$u:v:w \;=\; a:b:c \tag9$$ These are the barycentric coordinates of the incenter.

---

Addendum. Here' s an alternative representation of the above in terms of ratios $\alpha$, $\beta$, $\gamma$ such that $$ \overrightarrow{BD}\;=\;\alpha\,\overrightarrow{BC}\qquad \overrightarrow{CE}\;=\;\beta\,\overrightarrow{CA}\qquad \overrightarrow{AF}\;=\;\gamma\,\overrightarrow{AB} $$

That is, a ratio expresses how far along an edge one of these points is, with travel along the edges take to be in the directions $B\to C$, $C\to A$, $A\to B$. (OP mentions taking these ratios in the interval $[0,1]$, but there's no geometric or algebraic reason they can't be arbitrary real numbers: greater than one for traveling beyond the far endpoint of an edge, and less than zero for traveling the "opposite" direction.)

Then, making the substitutions $$ |BD|\to a\,\alpha \qquad |DC|\to a\,(1-\alpha) \\ |CE|\to b\,\beta \qquad |EA|\to b\,(1-\beta) \\ |AF|\to c\,\gamma \qquad |FB|\to c\,(1-\gamma)$$ into Carnot's relation gives $$a^2 + b^2 + c^2 \;=\; 2 \left(\; a^2\,\alpha \;+\; b^2\,\beta \;+\; c^2\,\gamma\;\right) \tag{1'}$$ which makes solving for one ratio in terms of the other two straightforward. (Sanity check: The relation holds for $\alpha=\beta=\gamma=\tfrac12$, as it should for the case where $P$ is the circumcenter.)

Further, defining $\alpha' :=1-\alpha$, etc, to reduce clutter, we find that $(3,4,5,6)$ become $$\begin{align} u &\;=\; a^2 \left(\;-a^2\,\alpha\alpha' \;+\; b^2\,\alpha\beta \;+\; c^2\,\alpha'\gamma'\;\right) \tag{3'}\\[4pt] v &\;=\; b^2 \left(\;-b^2\,\beta\beta' \;+\; c^2\,\beta\gamma \;+\; a^2\,\beta'\alpha'\;\right) \tag{4'}\\[4pt] w &\;=\; c^2 \left(\;-c^2\,\gamma\gamma' \;+\; a^2\,\gamma\alpha \;+\; b^2\,\gamma'\beta'\;\right) \tag{5'}\\[4pt] u+v+w &\;=\; 4\,|\triangle ABC|^2 \tag{6'} \end{align}$$ and we still have $$P \;=\; \frac{u}{u+v+w}\,A \;+\; \frac{v}{u+v+w}\,B \;+\; \frac{w}{u+v+w}\,C$$ where we can interpret the points as their coordinate vectors.

Answer 2

Here's a discussion that uses more explicit vector methods that may appeal to OP. I'm separating this from my previous answer to keep that one from getting too long, and because I'm changing a little bit of notation. (The second half of this answer will tie back to my previous answer.)

Suppose the vertices of $\triangle ABC$ have coordinates $$A = (A_x, A_y) \qquad B = (B_x, B_y) \qquad C = (C_x, C_y)$$ and suppose we erect perpendiculars along edges $BC$, $CA$, $AB$ at points $$P := B + p\,(C-B) \qquad Q := C + q\,(A-C) \qquad R := A+r\,(B-A)$$ for some scalar ratios $p$, $q$, $r$. Using just $P$ and $Q$, we can find $K=(K_x,K_y)$, the point of intersection of the perpendiculars, by solving the system $$(K-P)\cdot(B-C) \;=\; 0 \;=\; (K-Q)\cdot(C-A) \tag1$$ The result is ... a mess. With perseverance, we can group things to find that $$\begin{align} K_x &= C_x + \frac1t\left(\; + (1 - p) a^2\,(A_y - C_y) - q b^2\,(B_y - C_y)\;\right) \tag2 \\[4pt] K_y &= C_y + \frac1t\left(\; - (1 - p) a^2\,(A_x - C_x) + q b^2\,(B_x - C_x)\right) \tag3 \\[6pt] t &:= A_y B_x - A_x B_y - A_y C_x + B_y C_x + A_x C_y - B_x C_y \tag4 \end{align}$$ The similarity of the expressions suggests that we're doing something right; the mis-match of $x$- and $y$-coordinates, and signs, suggests that we have an opportunity to do something right-angled.

Define $(x,y)^\perp = (y,-x)$, which rotates a vector counter-clockwise by $90^\circ$. With this, we can combine the coordinate expressions above into a single a vector relation:

$$\overrightarrow{CK} \;=\; \frac1t \left(\;(1-p)a^2\,\overrightarrow{CA}^{\,\perp} \;-\; qb^2\,\overrightarrow{CB}^{\,\perp}\;\right) \;=\; \frac1t \left(\;(1-p)a^2\,\overrightarrow{CA} \;-\; qb^2\,\overrightarrow{CB}\;\right)^{\perp} \tag{$\star$}$$

This allows us to calculate the displacement of the target point $K$ relative to vertex point $C$. As a practical matter, we're done.

As a mathematical matter, the asymmetry of $(\star)$ is rather unappealing. One way to remedy this issue is to express (the coordinates of) $K$ as a weighted average of vertices $A$, $B$, $C$; eg,

$$K = \frac{1}{u+v+w}\left(\;u A + v B + w C\;\right) \tag5$$ for some weights $u$, $v$, $w$, where the arithmetic happens coordinate-wise, just like with vectors. To get the weights, we treat $(5)$ as a homogeneous system of two coordinate equations, solve, and simplify.

Using $K_x$ and $K_y$ as in $(2)$ and $(3)$, we find (with a bit of work) $$\begin{align} u:v:w &\quad=\quad 2 a^2 \left(\; 2 b^2 q - (1 - p) (-c^2 + a^2 + b^2) \;\right) \\ &\quad\quad :\; 2 b^2 \left(\; 2 (1 - p) a^2 - q (-c^2 + a^2 + b^2) \;\right) \\ &\quad\quad :\; (-b^2 + c^2 + a^2) (-c^2 + a^2 + b^2) + 2 p a^2 (-a^2 + b^2 + c^2) - 2 q b^2 (-b^2 + c^2 + a^2) \end{align} \tag6$$ This is still woefully asymmetric, and with good reason: it only incorporates two of the three parameters $p$, $q$, $r$. Referring to Carnot relation $(1')$ in my previous answer (and reading $\alpha$, $\beta$, $\gamma$ as $p$, $q$, $r$), we can massage the above into $$\begin{align} u:v:w &\quad=\quad a^2 \left(-a^2 p (1 - p) + b^2 p q + c^2 (1 - p) (1 - r)\right) \\ &\quad\quad :\; b^2 \left(-b^2 q (1 - q) + c^2 q r + a^2 (1 - q) (1 - p)\right) \\ &\quad\quad :\; c^2 \left(-c^2 r (1 - r) + a^2 r p + b^2 (1 - r) (1 - q)\right) \end{align} \tag{$\star\star$}$$ which is equivalent to my previous answer's equations $(3',4',5')$, and implies $(6')$.

While longer than $(\star)$ above, $(\star\star)$ is fully symmetric in the triangle's elements, which is nice. (As a bonus, the weighted-average formula $(5)$ for $K$ works for a triangle floating in any number of dimensions. The "$\perp$" formulation is trickier to define outside of the $xy$-plane.)