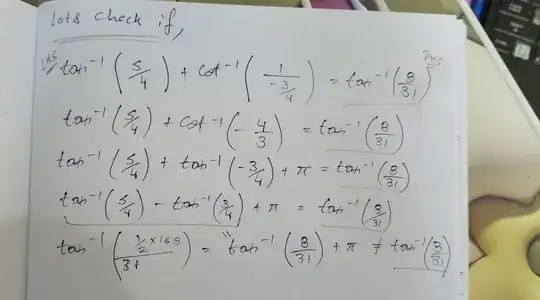7

$\tan^{-1}(x+1)+\cot^{-1}(\frac{1}{x-1})=\tan^{-1}(\frac{8}{31})$

One thing to clear is that the range of arccotangent is $(0,\pi)$. I am so sad because I can't use Wolfram to cross check my answers. I tried to solve the problem and got two values of $x=\frac{1}{4},-8$ But I had used the tangent function on both sides. So there were high chances that extraneous roots have been generated. So I tried to put $x=\frac{1}{4}$ and $-8$. But in both cases I came to the end value $\pi+\tan^{-1}(\frac{8}{31})$ which is not equal to $\tan^{-1}(\frac{8}{31})$

Moreover to my surprise both the answer are given as the correct answers in the answer key. I don't trust it though.

Please guide me where I am going wrong.

The issue is the arccotangent's range. Or it would have been way easier.

Edit 1: My solution:

enter image description here

Edit 2: Check if x= 1/4 is valid or not enter image description here

Darshit Sharma
  • 93
  • Wolfram gives the answer as $\frac{1}{4}$ only. I will post a longer answer if anything comes to me. – Red Five May 13 '24 at 05:24
  • @RedFive Ya I saw that sir... – Darshit Sharma May 13 '24 at 05:30
  • Let's see what I could come upto with the range $(\frac{-\pi}{2},\frac{\pi}{2})$....just solving to see if my answers match with wolfram's. However the original question is with the range mentioned in the question only. – Darshit Sharma May 13 '24 at 05:32
  • All good - it is a nice problem. I am wondering if a sketch of a triangle may help somehow. Will post it as an answer if I get anywhere. – Red Five May 13 '24 at 05:32
  • Sure sir @RedFive Eagerly waiting for your solution :) – Darshit Sharma May 13 '24 at 05:33
  • 1
    No promises... I'll see what can be done though. I'm guessing the two answers you found came from forming and solving a quadratic in x? – Red Five May 13 '24 at 05:34
  • Yes sir @RedFive – Darshit Sharma May 13 '24 at 05:50
  • Wolfram is not showing the answer -8 because it doesn't satisfies the equation if we take the range of arccotangent from -pi/2 to pi/2 – Darshit Sharma May 13 '24 at 05:54
  • 1
    However the original ques was and is concerned with arccotangent range from 0 to pi, which indeed justifies the issue I mentioned in my ques (that extra +pi) – Darshit Sharma May 13 '24 at 05:57
  • afaik, Wolfram alpha takes the range of arccot from 0 to pi – Blue Cat Blues May 13 '24 at 07:12
  • @MathStackexchangeIsNotSoBad No Sir it treats arccot as a odd function which isn't possible on 0 to pi – Darshit Sharma May 13 '24 at 08:03
  • @DarshitSharma I guess you're right...i plugged arccot(-root3) in Wolfram and it gave -pi/6....let me solve it...maybe then 1/4 won't come as an answer according to the domain of 0 to pi – Blue Cat Blues May 13 '24 at 14:29
  • @DarshitSharma i solved it...and guess what...-8 is a solution and 1/4 isn't – Blue Cat Blues May 13 '24 at 14:44
  • Personally, I would have approached the problem very differently, by working exclusively with arctan, and dispensing with any need to consider arccot. This is easily done by considering the two separate cases of $~(x - 1) > 0,~$ and $~(x - 1) < 0.~$ When $~(x - 1) > 0,~$ you have that $$\text{arccot}\left(\frac{1}{x-1}\right) = \text{arctan}(x-1).$$ When $~(x - 1) < 0,~$ you have that $$\text{arccot}\left(\frac{1}{x-1}\right)= \text{arctan}(x-1) + \pi.$$ – user2661923 May 13 '24 at 18:06
  • Wolfram spits out $x=\frac14$ because it treats the LHS like$$\tan^{-1}\left(\frac x2-\frac1x\right)+\frac\pi2\operatorname{sgn}(x)$$whereas, using your definition of $\cot^{-1}$, I think it should end up equivalent to$$\begin{cases}\tan^{-1}\left(\frac x2-\frac1x\right)+\frac{3\pi}2&x>0\\tan^{-1}\left(\frac x2-\frac1x\right)+\frac\pi2&x<0\end{cases}$$ – user170231 May 13 '24 at 18:52
  • @user170231 Yeah sir, I have solved using both definitions, if we use mine x= -8 and if we use wolfram's x=1/4 – Darshit Sharma May 13 '24 at 19:05

1 Answers1

2

This is not a full answer. I'll post the full fledged one if OP wishes. Kinda similar to the existing one tho.

First solve for the case when $x>1$

Then solve when $x\le-1$

And finally when $-1\le x<1$

When $x>1$

We have, $$\arctan(x+1)+\operatorname{arccot}\left(\frac{1}{x-1}\right)=\arctan\left(\frac{8}{31}\right)$$ $$\implies \arctan(x+1)+\arctan(x-1)=\arctan\frac{8}{31}$$ Solving this gives $x=\frac14$ or $x=-8$ but we must have $x>1$ so none of them are valid.

When $x<-1$

Let $x=-k$ where $k$ is a positive real number greater than $1$. Rewrite the equation as $$\arctan(1-k)+\operatorname{arccot}\left(\frac{1}{-k-1}\right)=\arctan\frac{8}{31}$$ $$\implies -\arctan(k-1)+\pi-\operatorname{arccot}\left(\frac{1}{k+1}\right)=\arctan\frac{8}{31}$$ $$\implies \pi-\arctan\frac{8}{31}=\arctan(k+1)+\arctan(k-1)$$ We now have all arguments positive so we can apply the basic formula here.

After solving we get $k=8$ as solution or $x=-8$

Since $x$ must be $<-1$, this is a valid solution.

Hence the solution of this equation is $$\boxed{x=-8}$$

I leave it to the OP to solve for the left case.

Blue Cat Blues
  • 10,058