Note: I feel the question is ultimately too vague to have a "proper" answer, but this is definitely too long for a comment.
Ultimately, it just really depends. Taylor series would be the go-to, just because of how often these series crop up and how easy integrating polynomials is, if you want a quick-and-dirty brute-forcing type of approach. Here,
$$
\sin x^2 = \sum_{n=0}^\infty \frac{(-1)^n x^{4n+2}}{(2n+1)!}
$$
Integrating polynomials is easy, and for Taylor series you can interchange integrals and sums just fine within the radius of convergence. So
$$\begin{align*}
\int_0^2 \sin x^2 \, \mathrm{d}x
&= \int_0^2 \sum_{n=0}^\infty \frac{(-1)^n x^{4n+2}}{(2n+1)!} \, \mathrm{d}x\\
&= \sum_{n=0}^\infty \int_0^2 \frac{(-1)^n x^{4n+2}}{(2n+1)!} \, \mathrm{d}x\\
&= \sum_{n=0}^\infty \frac{(-1)^n }{(2n+1)!} \int_0^2 x^{4n+2}\, \mathrm{d}x\\
&= \sum_{n=0}^\infty \frac{(-1)^n }{(2n+1)!} \frac{1}{4n+3} 2^{4n+3}
\end{align*}$$
To finish, then, you would examine
$$
\sum_{n=0}^N \frac{(-1)^n }{(2n+1)!} \frac{1}{4n+3} 2^{4n+3}
$$
for $N$ sufficiently large; what constitutes "sufficiently large" depends on how good of an approximation you need. For some small $N$,
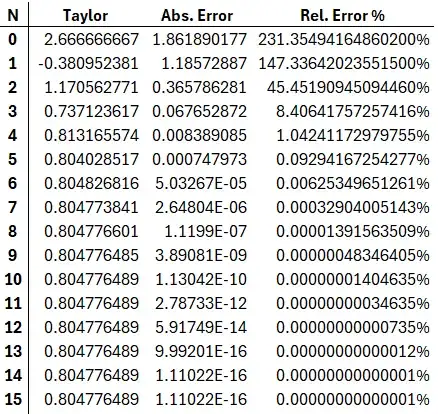
(This table, of course, assumes you know the exact value outright, but is more of a means to show the convergence rate. If you have conditions like "$n$ digits of precision," or "error less than $x$ amount", then you will have to do further analysis, e.g. like here.)
That said, other estimation methods and concerns might arise in other contexts, e.g. speed of convergence. Some of the more basic ones can be found here (midpoint, trapezoid, & Simpson's rules), which work by approximating the function to-be-integrated by constant, linear, and quadratic functions respectively. There is also a Simpson's second rule which uses interpolation by cubics (Wikipedia), and more generally the Newton-Cotes rules (Wikipedia), just to get you started. Taylor's theorem may also be of interest.
