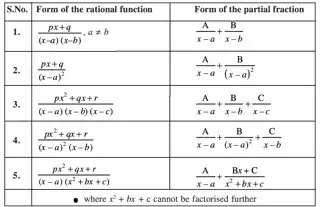
Before, integrating, we can often split a fraction into its partial fractions to make the integration process significantly more simple. However, I have realised that this fraction we can split can take on various forms.
Although, I can easily remember these forms for partial fractions given each case, I want to know the intuition behind it. Consider number 1. It makes sense that to add these two fractions, we can make the denominator the same, and the resulting numerator will be linear. However consider number 2, can number 2 not be expressed as the previous case, but now we have a squared term on one of the partial fractions. Why?
I am looking for intuition to determine the denominator of partial fractions. I don't want to remember all of these, but rather, when given an algebraic fraction, already be able to determine the form of the partial fractions and the intuition for this. Conside case 5, how come now the numerator is $Bx+C$?