I was looking at the zero's of
$$f(s,a) = \sum_{n=1}^{a-1} n^{-s} $$
for integer $a>3$ in the strip $0 < \operatorname{Re}(s) < 1$.
Now this clearly relates to the Riemann zeta:
$$f(s,a) + \zeta(s,a) = \zeta(s)$$
where $\zeta(s,a)$ is the hurwitz zeta function.
Notice the limits $f(s,+\infty)$ and $\zeta(s,+\infty)$ do not converge to functions of $s$, yet their sums do ; the Riemann zeta function. Nevertheless these function do have zero's for every $a>3$.
For small $a$ the zero's seem to be somewhat random in the strip $0 < \operatorname{Re}(s) < 1$.
But for large $a$ we seem to get some patterns.
For some unbounded function $0 < g(a) < a$ and $s = x + g(a)i$ with $0 < x < 1$ we get that the zero's of $f(s,a)$ are all the strip $1/2 < \operatorname{Re}(s) < 1$.
It seems the line $\operatorname{Re}(s) = 1/2$ is attracting the zero's for large $g(a)$ but for small imaginary parts it seems it is in fact repelling.
So it seems the zero's are dense on a curve (looks continuous but like lightning) within $1/2 < \operatorname{Re}(s) < 1$ that tends towards the line 1/2, but is not smooth and is repelled from 1/2 for small imaginary parts.
I assume the positions of the zeros of $f(s,a)$ converge as $a$ grows or at least the curve they are on does converge to a fixed curve/path.
It surprised me that $a$ needed to be so big to get apparant converge of the zero's towards $1/2 < \operatorname{Re}(s) < 1$ and towards that curve/path.
Is all this a consequence of the Riemann Hypothesis ? Is it a stronger statement ? Or a weaker statement ?
The following post illuminates some aspects, in particular for $1/2 + r i$ with $r$ large and the zero's on that line. But that is just a part.
To clarify I will post a picture of $f(s,20000)$ made with sage 9.2.
t(x)=hurwitz_zeta(x,1)-hurwitz_zeta(x,20000)
complex_plot(t(x),(0,0.99),(-2,20))
enter
Is there a closed form for this curve/path ?
Clarifications would be nice.
I did not look at the zero's of the counterpart $\zeta(s,a)$ ... maybe I should ?
Can contour integrals solve this ?
Or other expressions for $\zeta(s)$ ?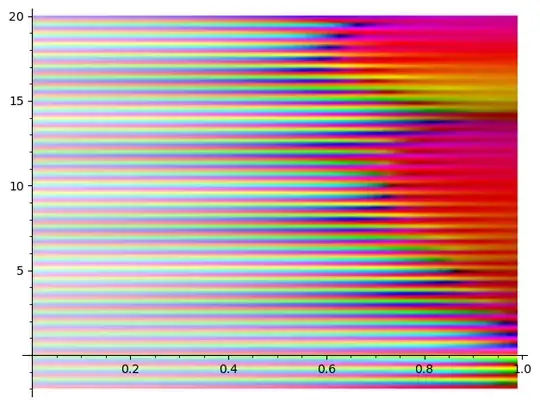
This paper gives some additional insights :