Analytical solution of the equation for the launch angle of a projectile travelling the maximum trajectory length

Question

I would like to find an analytical solution to the equation by which the launch angle is found for a projectile to travel the maximum trajectory length.

Let $\theta$ be the angle at which the ball is thrown. Then the coordinates are given by $$ x = (v \cos \theta )t\quad\mbox{and}\quad y = (v \sin \theta )t − {gt^2 \over 2} $$ The ball reaches its maximum height at $t = v \sin \theta/g$, so the length of the trajectory is

$$L = 2 \int^{v \sin \theta/g}_{0}\sqrt{\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2 + \left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2 \mathrm{d}t} = 2 \int^{v \sin \theta/g}_{0}\sqrt{(v \cos \theta)^2 + (v \sin \theta - gt)^2} \ \mathrm{d}t = 2v\cos \theta \int^{v \sin \theta/g}_{0} \sqrt{1 + \left(\tan \theta - \frac{gt}{v \cos \theta}\right)^2} \ \mathrm{d}t \ .$$

We can solve this integral by substitution, and eventually, after differentiating ($\frac{\mathrm{d}L}{\mathrm{d}\theta} = 0$) obtain the equation

$$\sin \theta \ln \left(\frac{1 + \sin \theta}{\cos \theta}\right) = 1 \ .$$

You can show numerically that the solution for $\theta$ is $\theta_0 \approx 56.5^\circ$ (I performed the calculation with Mathematica), but is there a way to solve this equation for $\theta$ analytically?

P.S. This, this and this arrive at a different equation, but the performed numerical result is the same. Once again, I have yet to see an analytical resolution.

Answer 1

I struggle to give a precise definition of the concept of an analytical solution of a specific problem. Usually, it a short formula that in principle allows us to compute the exact value of the solution, but frequently the formula is useless for practical calculations and it real value is two-fold. It proves beyond any doubt the existence of the solution and it allows us to probe properties of the solution.

It is usually hard to derive analytical solutions and harder still to prove that they do not exists. In this case, I have only my intuition to suggest that no analytical solution exists. Instead I shall concentrate on finding a numerical solution and estimating the error. Moreover, I shall discuss some of the practical and real life concerns associated with application of numerical methods.

Our objective is solve the equation $f(x) = 0$ where \begin{equation} f(x) = \sin(x) \log\left(\frac{1 + \sin(x)}{\cos(x)}\right) - 1 \end{equation} Here $0 < x < \frac{\pi}{2}$ is the elevation for a piece of artillery. The natural domain of $f$ is therefore the open interval $I = (0,\pi/2)$. We observe that $f$ is continuous and it is straightforward to verify that $$ f(x) \rightarrow -1, \quad x \rightarrow 0, \quad x > 0$$ while $$ f(x) \rightarrow \infty \quad x \rightarrow \frac{\pi}{2}, \quad x < \frac{\pi}{2}.$$ This is also consistent with the following plot of the graph of $f$.

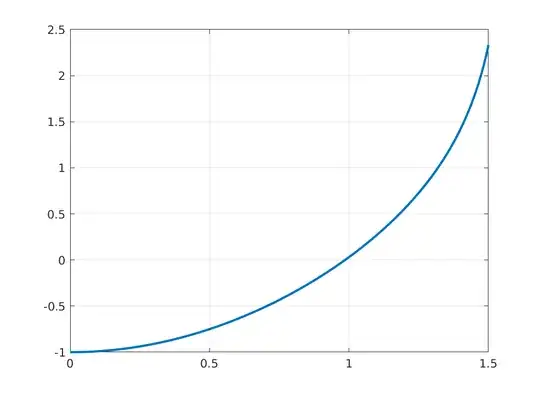
Moreover, we have that $$ f(0.5) \approx -0.7496$$ and $$ f(1.5) \approx 2.3323.$$ We conclude that the continuous function $f$ changes sign on the interval from $a = \frac{1}{2}$ to $b = \frac{3}{2}$. By the intermediate value theorem there must necessarily be at least one $z\in (a,b)$ such that $f(z) = 0$. We say that at $a$ and $b$ from a bracket around the zero $z$. We can systematically refine the bracket using the bisection method. We obtain a table similar to this one below. Here the $i$th row contains specifies numbers $a_i < b_i$ such that $f(a_i)$ and $f(b_i)$ have different sign, the approximation of the root $z$ is $c_i$ is the average of $a_i$ and $b_i$ and the residual is the value $f(c_i)$.

  iter |                      a |                      b |          approximation |               residual
     1 |  5.000000000000000e-01 |  1.500000000000000e+00 |  1.000000000000000e+00 |  3.180429212610059e-02
     2 |  5.000000000000000e-01 |  1.000000000000000e+00 |  7.500000000000000e-01 | -4.327615808338594e-01
     3 |  7.500000000000000e-01 |  1.000000000000000e+00 |  8.750000000000000e-01 | -2.214641585595649e-01
     4 |  8.750000000000000e-01 |  1.000000000000000e+00 |  9.375000000000000e-01 | -1.006252182840196e-01
     5 |  9.375000000000000e-01 |  1.000000000000000e+00 |  9.687500000000000e-01 | -3.595212429621009e-02
     6 |  9.687500000000000e-01 |  1.000000000000000e+00 |  9.843750000000000e-01 | -2.472954602789290e-03
     7 |  9.843750000000000e-01 |  1.000000000000000e+00 |  9.921875000000000e-01 |  1.456405888954038e-02
     8 |  9.843750000000000e-01 |  9.921875000000000e-01 |  9.882812500000000e-01 |  6.020388010089972e-03
     9 |  9.843750000000000e-01 |  9.882812500000000e-01 |  9.863281250000000e-01 |  1.767454829462833e-03
    10 |  9.843750000000000e-01 |  9.863281250000000e-01 |  9.853515625000000e-01 | -3.543117490389935e-04
    11 |  9.853515625000000e-01 |  9.863281250000000e-01 |  9.858398437500000e-01 |  7.061806255597158e-04
    12 |  9.853515625000000e-01 |  9.858398437500000e-01 |  9.855957031250000e-01 |  1.758367658362125e-04
    13 |  9.853515625000000e-01 |  9.855957031250000e-01 |  9.854736328125000e-01 | -8.926190268687684e-05
    14 |  9.854736328125000e-01 |  9.855957031250000e-01 |  9.855346679687500e-01 |  4.328132792608130e-05
    15 |  9.854736328125000e-01 |  9.855346679687500e-01 |  9.855041503906250e-01 | -2.299181318310417e-05
    16 |  9.855041503906250e-01 |  9.855346679687500e-01 |  9.855194091796875e-01 |  1.014437590729500e-05
    17 |  9.855041503906250e-01 |  9.855194091796875e-01 |  9.855117797851562e-01 | -6.423814002287642e-06
    18 |  9.855117797851562e-01 |  9.855194091796875e-01 |  9.855155944824219e-01 |  1.860257111241381e-06
    19 |  9.855117797851562e-01 |  9.855155944824219e-01 |  9.855136871337891e-01 | -2.281784405977483e-06
    20 |  9.855136871337891e-01 |  9.855155944824219e-01 |  9.855146408081055e-01 | -2.107651374538833e-07
    21 |  9.855146408081055e-01 |  9.855155944824219e-01 |  9.855151176452637e-01 |  8.247456144694354e-07
    22 |  9.855146408081055e-01 |  9.855151176452637e-01 |  9.855148792266846e-01 |  3.069901455265978e-07
    23 |  9.855146408081055e-01 |  9.855148792266846e-01 |  9.855147600173950e-01 |  4.811248066616258e-08
    24 |  9.855146408081055e-01 |  9.855147600173950e-01 |  9.855147004127502e-01 | -8.132633411150891e-08
    25 |  9.855147004127502e-01 |  9.855147600173950e-01 |  9.855147302150726e-01 | -1.660692794391849e-08
    26 |  9.855147302150726e-01 |  9.855147600173950e-01 |  9.855147451162338e-01 |  1.575277575049938e-08
    27 |  9.855147302150726e-01 |  9.855147451162338e-01 |  9.855147376656532e-01 | -4.270762632430092e-10
    28 |  9.855147376656532e-01 |  9.855147451162338e-01 |  9.855147413909435e-01 |  7.662849688117035e-09
    29 |  9.855147376656532e-01 |  9.855147413909435e-01 |  9.855147395282984e-01 |  3.617886878970467e-09
    30 |  9.855147376656532e-01 |  9.855147395282984e-01 |  9.855147385969758e-01 |  1.595405363374880e-09
    31 |  9.855147376656532e-01 |  9.855147385969758e-01 |  9.855147381313145e-01 |  5.841644945547841e-10
    32 |  9.855147376656532e-01 |  9.855147381313145e-01 |  9.855147378984839e-01 |  7.854406014473625e-11
    33 |  9.855147376656532e-01 |  9.855147378984839e-01 |  9.855147377820686e-01 | -1.742658239933803e-10
    34 |  9.855147377820686e-01 |  9.855147378984839e-01 |  9.855147378402762e-01 | -4.786093743547326e-11
    35 |  9.855147378402762e-01 |  9.855147378984839e-01 |  9.855147378693800e-01 |  1.534172788808519e-11
    36 |  9.855147378402762e-01 |  9.855147378693800e-01 |  9.855147378548281e-01 | -1.625977130714773e-11
    37 |  9.855147378548281e-01 |  9.855147378693800e-01 |  9.855147378621041e-01 | -4.590772206825022e-13
    38 |  9.855147378621041e-01 |  9.855147378693800e-01 |  9.855147378657421e-01 |  7.441380844852574e-12
    39 |  9.855147378621041e-01 |  9.855147378657421e-01 |  9.855147378639231e-01 |  3.491207323236267e-12
    40 |  9.855147378621041e-01 |  9.855147378639231e-01 |  9.855147378630136e-01 |  1.516120562428114e-12
    41 |  9.855147378621041e-01 |  9.855147378630136e-01 |  9.855147378625588e-01 |  5.286882043264995e-13
    42 |  9.855147378621041e-01 |  9.855147378625588e-01 |  9.855147378623315e-01 |  3.463895836830488e-14
    43 |  9.855147378621041e-01 |  9.855147378623315e-01 |  9.855147378622178e-01 | -2.121636200058674e-13
    44 |  9.855147378622178e-01 |  9.855147378623315e-01 |  9.855147378622746e-01 | -8.859579736508749e-14
    45 |  9.855147378622746e-01 |  9.855147378623315e-01 |  9.855147378623030e-01 | -2.697841949839130e-14
    46 |  9.855147378623030e-01 |  9.855147378623315e-01 |  9.855147378623172e-01 |  4.218847493575595e-15
    47 |  9.855147378623030e-01 |  9.855147378623172e-01 |  9.855147378623101e-01 | -1.154631945610163e-14
    48 |  9.855147378623101e-01 |  9.855147378623172e-01 |  9.855147378623137e-01 | -3.774758283725532e-15
    49 |  9.855147378623137e-01 |  9.855147378623172e-01 |  9.855147378623155e-01 |  2.220446049250313e-16

If we examine the last line of the table, we find that $$c_{49} = 9.855147378623155 \times 10^{-1}$$ with $$f(c_{49}) = 2.220446049250313 \times 10^{-16}$$ and it appears plausible that the zero is $$z \approx 9.855147378623155 \times 10^{-1}.$$ Why is it so plausible? There are two reasons to believe this. One is valid, the other is currently unsupported by fact. If we trust the program that generated the table, then $f(a_{49})$ and $f(b_{49})$ have different sign and since $c_{49}$ is the average of $a_{49}$ and $b_{49}$ it is the best available approximation. At this point, there is no reason to trust the program and so we consider an alternative. We have reason to believe that the zero is near 1, but less than 1. Here the floating point values are separated by a distance of $u$, where $u$ is the unit roundoff, i.e. $\{1-2u, 1-u, 1\}$ is an explicit list of the three largest floating point numbers that are less than or equal to 1. Therefore the smallest absolute error that we can hope to achieve is $u$. If $|x - z| \leq u$ and $f(z) = 0$, then by Taylor's theorem $$ f(x) \approx f(z) + f'(z)(x - z) = f'(z)(x-z)$$ Since $|f'(1)| \approx 1.6$, we cannot expect our that residual $f(x)$ will be significantly smaller than $$|f(x)| \leq 2 u$$ when the absolute error is less than $u$. We used IEEE double precision to generate the table, so $u = 2^{-53} \approx 1.1 \times 10^{-16}$. We found that $f(c_{49}) \approx 2u$ and so we are inclined to believe that $z \approx c_{49}$. Finally, we note that plenty of other people have found that $z \approx 56.5^\circ$ which is fairly close to $c_{49}$. If we have made a mistake, then it is likely a subtle one.

It is dangerous to trust the all the figures shown and even if they were correct we would be fools to communicate 16 significant figures to the crew that will eventually fire the gun. There is no way the crew can set the elevation so accurately and if we provide them with useless information it can gradually erode their confidence in our ability to generate firing solutions.

There are two issues here. One is a matter of finite precision arithmetic and the other is a matter of context.

The bisection algorithm hinges on our ability to compute the correct sign. Given an interval $(a,b)$ such that $f(a)$ and $f(b)$ have different sign, we compute $c = a + (b-a)/2$ and evaluate $y = f(c)$. If $f(a)$ and $f(c)$ have different sign, then the new bracket is $(a,c)$. Otherwise the new bracket is $(c,b)$. In order to choose between the two brackets $(a,c)$ and $(c,d)$ we do not need the exact value of $y = f(c)$, we only need an approximation $\hat{y}$ which has the same sign as $y$. Can we actually achieve this simple goal? Below is a plot of the computed value of $(x,f(z+x))$ for $x \in (-1,1) \times 2^{-48}$ with 1025 equidistant sample points.

This is not graph of a strictly increasing differentiable function. What we are observing is the impact of the rounding errors associated with computing $f$. Regardless, the picture is better than most in the sense that the computed function is at least monotone increasing. Regardless, it is clear that there is a hard limit for how accurately we can compute the value of $z$.

What sort of accuracy should we settle for? The underlying application is external ballistics and it is unreasonable to assume that crew can choose an elevation with an accuracy that is better than 0.5 degrees. After all, artillery pieces are big and heavy and the battlefield is likely to be uneven, wet or covered in snow. But let us be fanatical about the accuracy and investigate if $$z = 9.86 \times 10^{-1}$$ is correctly rounded to 3 significant figures? Return to the table and examine the rows one by one. Row 16 has $a_{16} = 9.855041503906250 \times 10^{-1}$ and $b_{16} = 9.855346679687500 \times 10^{-1}$ and every number in the interval $(a_{16},b_{16})$ will round to $z = 9.86 \times 10^{-1}$. In short, the question reduces to the following: Do we trust the computed sign of $f(a_{16})$ and $f(b_{16})$? Strictly speaking, this question is impossible to answer without examining the details of exactly how $f$ is evaluated on our machine. Instead we ask if it is at least theoretically possible to get the correct signs. The answer is: yes. The expression for the relative condition number $$\kappa_f(x) = \left| \frac{x f'(x)}{f(x)} \right|$$ of $f$ is hideous and while it explodes at $x=z$ the condition number is a modest $O(10^4)$ for $x = a_{16}$ and $x = b_{16}$. It is extremely reasonable to assume that the relative error on $f(a_{16})$ and $f(b_{16})$ is about $10^{-12}$ because the calculations were done in IEEE double precision arithmetic for which the unit roundoff is $u \approx 10^{-16}$. Hence we trust signs of $f(a_{16})$ and $f(b_{16})$ and since they are different we are (fairly) certain that $z = 9.86 \times 10^{-1}$ is correct to the figures shown.

Answer 2

You are looking for the zero of function $$f(\theta)=\sin( \theta) \,\log \left(\frac{1 + \sin (\theta)}{\cos (\theta)}\right) - 1$$

Using the tangent half-angle substitution it boils down to $$g(x)=2 x \log \left(\frac{1+x}{1-x}\right)-(1+x^2)$$

Now $$\frac{1+x}{1-x}=\sqrt t \quad \implies \quad 2 (1+t)+(1-t) \log (t) =0 $$

Searching for the writing of this last equation which makes the plot the most linear, what was selected is $$h(t)=t\,\exp\left(2 \frac{1+t}{1-t} \right)-1$$

Starting at $t=0$, the first iterate of Householder method of order $d = 3$ is $$t_0=\frac{4+e^2}{\left(2+e^2\right) \left(6+e^2\right)}$$ $h(t_0) $ being negative and $h''(t_0)$ being positive, by Darboux theorem, $t_0$ is an underestimate of the solution.

Notice that, converted to decimals, $t_0=0.0905974$ while the solution is $t=0.0907763$.

Using it, without any calculation, using the first iterate of Newton-like methods of order $n$ we have fully explicit approximations which write $$t_{(n)}=\frac {\sum_{k=0}^{n-1} a_k\,e^{2k} } {\sum_{k=0}^{n} b_k\,e^{2k} } $$ For example $$t_{(5)}=\frac{5 \left(212+472 e^2+252 e^4+48 e^6+3 e^8\right)}{2268+7960 e^2+6660 e^4+2160 e^6+300 e^8+15 e^{10}}$$ is almost the solution (absolute error of $1.418\times 10^{-7}$).

Playing with the order of the method and converting to decimals $$\left( \begin{array}{cc} n & t_{(n)} \\ 2 & 0.13533528324 \\ 3 & 0.08780358893 \\ 4 & 0.09059742142 \\ 5 & 0.09077655679 \\ 6 & 0.09077748678 \\ 7 & 0.09077641998 \\ 8 & 0.09077628640 \\ 9 & 0.09077627810 \\ 10 & 0.09077627814 \\ \end{array} \right)$$