I'm doing some numerical experiments to test an integrator, and I got this plot, for the motion of 5 pendula, whose initial displacement differ by $10^{-6}$ radians away from straight up ($\theta_0 = \pi - d\theta$, where $d\theta\in(1,2,3,4,5)\times10^{-6}$). It seems like they're diverging from each other exponentially. I'm wondering if this is real, or if it's due to accumulated error in my integrator. this particular integrator has passed all the other tests I've thrown at it (energy is being conserved to within one part in $10^5$, and this behavior is not replicated for pendula that begin below $\theta_0 = \frac{\pi}{2}$).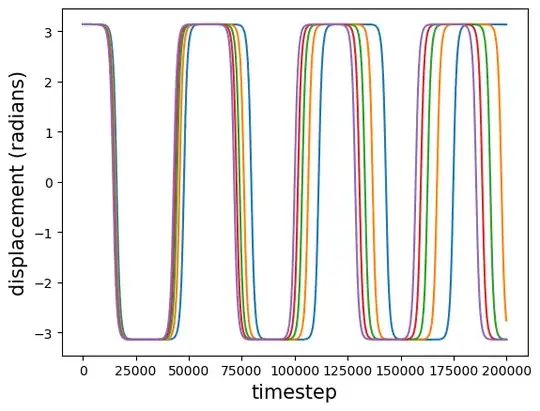
I'd be a little surprised if this is real, because I thought that the single pendulum has only negative or null lyapunov exponents. Is there something special about inverted pendula, maybe because their effective potential is an inverted hill at the top of their swing?