Statement about Homotopy in Brown's "Topology & Groupoids"

Question

I am trying to understand a statement in Brown's Topology and Groupoids, 7.2.5 (Corollary 1), page 270.

Let's first have some preliminary remarks

Let $X,Y$ be topological spaces. The track groupoid $\pi Y^X$ is defined as the groupoid whose objects are the maps $f:X\to Y$ and morphism in $\pi Y^X(f,g)$ are the homotopies $f\simeq g,$ where two homotopies $F,G$ are identified if they can be continuously deformed into each other while fixing the end maps. For $X=\{*\}$ we obtain the fundamental groupoid $\pi Y.$ A map $i:A\to X$ induces a morphism $i^*:\pi Y^X\to\pi Y^A$ by $i^*([F])=[F(i\times 1)].$

Let $i:A\to X,\ u:A\to Y.$ By $[(X,i),(Y,u)]$ we mean the set of homotopy classes of maps $f:X\to Y,fi=u,$ where a homotopy $F:f\simeq g$ is required to satisfy $F(ia,t)=ua.$ (We say $f$ and $g$ are homotopic under $i.$)

(You might want to skip this shaded part as it's probably not relevant for the particular question.):

Let $p : E → B$ be a morphism of groupoids. We say $p$ is a fibration if the following condition holds: for all objects $x$ of $E$ and elements $b$ in $B$ with initial point $px,$ there is an element $e$ of $E$ with initial point $x$ and such that $pe = b.$

If $p : E → B$ is a morphism of groupoids and $u$ is an object of $B,$ we write $p^{-1}[u]$ for the subgroupoid of $E$ with objects those $x$ in Ob$(E)$ such that $px = u,$ and with elements those $e$ in $E$ such that $pe = 1_u.$

Let $\pi_0G$ denote the set of components of $G.$ then we have:
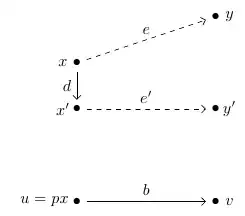
Lemma 1: If $p:E\to B$ is a fibration of groupoids, then for each $b\in B(u,v)$ there is a bijection $$b_\#:\pi_0 p^{-1}[u]\to\pi_0 p^{-1}[v]$$ which respects identities and composition. Namely, if $x$ is an object with $px=u$, we assign to the component of $x$ the component of the object $y$ which is the codomain of the element $e$ such that $pe=b.$

Lemma 2: A cofibration $i:A\hookrightarrow X$ induces a fibration $i^*:\pi Y^X\to\pi Y^A.$

Lemma 3: Let $i:A\hookrightarrow X$ be a cofibration. Let $u:A\to Y$ be a map. Let $p=i^∗:πY^X\to πY^A.$ Then there is a canonical bijection $$π_0 p^{−1}[u]\cong[(X, i), (Y, u)].$$

In the proof of the Lemma 3 we use the following fact. Maybe it turns out to be useful in solving my question:

Lemma 4: Let $i:A→X$ be a cofibration. Let $H:X\times\Bbb I→Y$ be a homotopy $f≃g,$ and let $G=H(i\times1)$ be homotopic rel end maps to $G′:u≃v.$ Then $H$ is homotopic rel end maps to some $H′:f≃g$ such that $H'(i\times 1)=G'.$

Now we can combine the three lemmas to derive the following

Corollary: Let $i:A\hookrightarrow X$ be a cofibration and $α\in πY^A(u,v).$ Then there is a bijection $$α_\#:[(X, i), (Y, u)] → [(X, i), (Y, v)] $$

I have figured out that this bijection works as follows:
Choose a representative $F$ of $\alpha.$ For a homotopy class $[f]$ take a representative $f:X\to Y,\ fi=u.$ The homotopy $F:u\simeq v$ on $A$ can be extended to a homotopy $G:f\simeq g'.$ Then we have $[g']=\alpha_\#([f]).$

Now, Brown writes

Also, if $α_\#([f]) = [g],$ then any representative of $α$ extends to a homotopy $f\simeq g.$

I don't see why this should be obvious. I know that if $F:u\simeq v,\ F\in\alpha,$ then there is an extension of $f\cup F$ to a homotopy $G:f\simeq g'$ for some $g:X\to Y,\ g'i=v.$ And this $g'$ is homotopic under $i$ to $g.$ But I don't see how these homotopies can be combined to a homotopy $f\simeq g$ which extends $F.$

Answer 1

The lemma 3 is deeper than it looks : in there you have to prove that if there is an homotopy $G : f \to g$ such that $i^*(G) = F : u \to u$ is homotopic to $id_u$, then there is an homotopy $G' : f \to g$ that is above $i$ and $u$.

From an homotopy $H : F \to id_u$ and a pullback $G : f \to g$ of $F$, you can pullback $H$ to an homotopy $H' : G \to G'$ such that $i^*(H') = H$. Hence $i^*(G') = id_u$ and so $G' : f \to g$ is an homotopy above $i$ and $u$.

And this is actually used when showing that the homotopy class of $\alpha_\sharp(f)$ is well-defined by your construction :

Suppose $F : u \to v$ and $f : X \to Y$ such that $i^*(f) = u$.

By lemma 2, $i^* : \pi Y^X \to \pi Y^A$ is a fibration, and $F$ can be pulled back : there is some $g \in i^{*-1}(v)$ and some $G : f \to g$ such that $F = i^*(G)$. We pick $F_\sharp(f) = g$.

By lemma 1, if there is an homotopy between $f$ and $f'$ above $i,u$, then there is an homotopy between $g$ and $g'$ above $i,v$. In particular (picking $id_f : f \to f$), if there are several possible $g$ for the same $f$, they are homotopic : if $G : f \to g$ and $G' : f \to g'$ are two pullbacks of $F$, then $G' G^{-1} : g \to g'$ is an homotopy whose image by $i^*$ is $F F^{-1}$. This is not $id_v$ so this homotopy is not above $i$ and $v$. However, $F F^{-1}$ is homotopic to $id_v$. As it should be explained in lemma 3, you can pullback this starting from $G'G^{-1}$ to obtain a new homotopy $g \to g'$ whose image by $i^*$ is $id_v$, which means it is above $i$ and $v$.

Hence even though $g = F_\sharp(f)$ itself is not fully determined, its homotopy class is, and depends only on the homotopy class of $f$.

What's left is to show that if we pick another $F'$ homotopic to $F$ then $g'$ is homotopic to $g$ above $i$ and $v$, (and in fact, $G$ is homotopic to $G'$)

---

You can prove straight from lemma 3 that if $\alpha = [id_u]$ then $\alpha_\sharp([f]) = [f]$ forall $[f] \in [(X,u),(Y,u)]$ :

If $H : F \to id_u$ in $\pi Y^A(u,u)$ and if you have a pullback $G : f \to g$ of $F$, this is an actual arrow in $i^{*-1}(u)$ (since $i^*G = F \equiv id_u$). Hence $f$ and $g$ are in the same component in $\pi_0i^{*-1}(u)$. By lemma 3, they are in the same homotopy class above $i$ and $u$, and so $[f] = [g]$ (again, we pullback the homotopy between $F$ and $id_U$ starting from $G$ to get a new homotopy from $f$ to $g$ which is above $i$ and $u$)

Hence $id_{u\sharp} = id_{[(X,u),(Y,u)]}$. You can then argue that $F_\sharp G_\sharp = (FG)_\sharp$ and $(F_\sharp)^{-1} = (F^{-1})_\sharp$, then use the fact that if $F$ and $G$ are homotopic, then $G^{-1}F$ is homotopic to $id_U$, and conclude from there that $F_\sharp = G_\sharp$.

---

You can also do this by doing an actual pullback straight from the homotopy :

Suppose $F_1,F_2 : u \to v$, $H : F_1 \to F_2$ is an homotopy and $f : X \to Y$ satisfies $i^*(f) = u$.

Then we can pullback $F_1$ to an homotopy $G_1 : f \to g$ where $i^*(g) = v$ and $i^*(G_1) = F_1$. Then we can pullback $H$ to an homotopy $H' : G_1 \to G_2$ where $i^*(H') = H$ hence $i^*(G_2) = F_2$. So $G_2 : f' \to g'$ where $i^*(f') = u$ and $i^*(g') = v$.
The faces of $H'$ give you an homotopy $f \to f'$ above $i$ and $u$, an homotopy $g \to g'$ above $i$ and $v$. Combining those with $G_1$ or $G_2$ give homotopies between $f$ and $g$ (you can have one above $F_1$ and one above $F_2$), and they are homotopic (because $H'$ is the homotopy between them)

---

So we have a well-defined map between homotopy classes of homotopies $F : u \to v$ and homotopy classes of $f$ above $u$, to homotopy classes of $g$ above $v$, and in fact to homotopy classes of homotopies $G : f \to g$,

Answer 2

I have finally figured it out. The solution is to look carefully at the proof of Lemma 1 and its implications.

Assume that $b\in B(u,v)$. Let $x$ be an object in $p^{-1}[u]$, that is $px=u$. As $p$ is a fibration, there is an arrow $e$, starting at $x$ and ending at an object which we will denote $y$, such that $pe=b$. Then we can define $b_\#(\bar x)=\bar y$. Of course, we have to check this is well-defined. To this end, let $x'$ be another object in $\bar x$, and let $e'$ be an arrow in $E(x',y')$ with $pe'=b$. Then there is a morphism $d:x\to x'$ such that $pd=1_u$. Now, $e'de^{-1}$ is an arrow from $y$ to $y'$ and $p(e'de^{-1})=b1_yb^{-1}=1_v$. That means that $y$ and $y'$ are in the same component of $p^{-1}[v]$. So the action of $B$ on $\pi_0p^{-1}[u]$ is well-defined. $\square$

Additionally, if $b_\#(\bar x)=\bar y$, then there is an arrow $e$, starting at $x$ and ending at some $y'$ such that $pe=b$ and $\bar y'=\bar y$. But then there is also an arrow $d:y'\to y$ with $pd=1_v$. The composition $de$ maps to $b$. So we can say that $b_\#(\bar x)=\bar y$ if and only if some arrow from $x$ to $y$ lifts $b$.

---

Now, if $i:A↪X$ is a cofibration and $u:A→Y$ a map, then $p:=i^*:πY^X→πY^A$ is a fibration. Further, $πY^A$ operates on the family of sets $π_0 p^{-1}[u],\ u:A\to Y$ via $α_\#\bar x=\bar y$.
To answer the question, assume that $α_\#\bar f=\bar g$ and that $H:u≃v$ is an element in $α$. Then there is an arrow $β∈πY^X(f,g)$ which maps to $α$ via $p$. If $K:f≃g$ is a representative of $\beta$, then $pβ=α$ means that $K(i×1)$ is homotopic rel $u,v$ to $H.$ The lemma 4 in my question then asserts that $K$ is homotopic rel $f,g$ to a homotopy $K':f≃g$ which extends $H$. This shows that if $α_\#\bar f=\bar g$, any representative $H$ of $α$ can be extended to a homotopy $f≃g$.

In particular, we can take $α=1_u$ represented by the homotopy $H$ of lenght $r$ such that $H(a,s)=u(s)$. Then $α_\#(\bar f)=\bar g$ iff $f$ and $g$ are in the same component of $p^{-1}[u]$. By the above result the constant homotopy $H:u≃u$ can be extended to a homotopy $K:f≃g$, which means that $f$ and $g$ are homotopic under $A$ and thus they are in the same homotopy class of $[(X,i),(Y,u)]$. That's why we have a bijection $$π_0p^{−1}[u]≅[(X,i),(Y,u)]$$ and, consequently, $πY^A$ acts on the set of homotopy classes: $$α_\#:[(X,i),(Y,u)]\to[(X,i),(Y,v)]$$

Answer 3

Let $i:A\rightarrow X$ be a cofibration and $Y$ a topological space. With 7.2.5 (Lemma) on page 269 we find:

$\text{cls }H\left(i\times1\right)=\left\{ H'\left(i\times1\right)\mid H'\in\text{cls }H\right\} $ for every homotopy $H:X\times\mathbb{I}\rightarrow Y$.

Let $F:u\simeq v$ for $u,v:A\rightarrow Y$ and $fi=u$.

Let $\alpha:u\rightarrow v$ be an arrow in $\pi Y^{A}$ represented by $F$ (i.e. $\alpha=\text{cls }F$) and let $g$ be a representative of $\alpha_{\#}\left[f\right]$ here (i.e. $\alpha_{\#}\left[f\right]=\left[g\right]$).

Since $i^{*}:\pi Y^{X}\rightarrow\pi Y^{A}$ is a fibration there is an arrow $\text{cls }H:f\rightarrow g$ in $\pi Y^{X}$ with $i^{*}\left(\text{cls }H\right)=\text{cls }F=\alpha$. So $\alpha=\text{cls }H\left(i\times1\right)=\left\{ H'\left(i\times1\right)\mid H'\in\text{cls }H\right\} $ wich means that $F=H'\left(i\times1\right)$ for some $H':f\simeq g$