Determine the rotation necessary to make a line tangent to an ellipse

Question

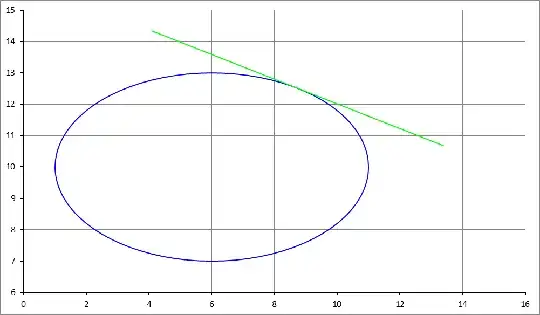
Question:

Given the line

$ \ell(t) = r_0 + t \ u $

I want to rotate it about point $P_0$, such that it becomes tangent to the ellipse

$ (r - C)^T Q (r - C) = 1$

where $ r = [x,y]^T$, $C$ is the center of the ellipse, and $Q$ is $2 \times 2 $ symmetric positive definite matrix.

My attempt:

Rotation of the given line about $P_0$ by an angle $\theta$ produces the new line

$ L(t) = P_0 + R (\ell(t) - P_0) = P_0 + R ( r_0 - P_0 + t \ u ) $

Let $n$ be perpendicular to $u$ , then $ R n $ is the normal vector of the rotated line.

The point $r_1$ on the ellipse where the gradient is parallel to this normal vector of the rotated line satisfies

$ Q (r_1 - C) = K R n $

It can be easily shown that

$ K = \dfrac{1}{\sqrt{ n^T R^T Q^{-1} R n } } $

Hence

$ r_1 = C + \dfrac{ Q^{-1} R n }{ \sqrt{ n^T R^T Q^{-1} R n }} $

Now we want this point to be on the line, therefore, we want

$ ( R n )^T ( r_1 - [ P_0 + R ( r_0 - P_0) ] ) = 0 $

Substituting $r_1$ gives

$ (R n)^T ( C - P_0 - R (r_0 - P_0) ) + \sqrt{ n^T R^T Q^{-1} R n } = 0 $

Therefore, we want to solve

$ n^T R^T Q^{-1} R n = \bigg( (R n)^T (C - P_0) - n^T (r_0 - P_0) \bigg)^2 $

Define $w = R n$ , and $ V = C - P_0 $, and $ c_0 = n^T (r_0 - P_0) $

Then the above equation is

$ w^T (Q^{-1} - {VV}^T ) w + 2 c_0 w^T V - c_0^2 = 0 $

We can assume that $n$ is a unit vector, then so is $w$, i.e.

$ w^T w = 1 $

Solving these two equations gives $w$. Now we can find $\theta$ which related the rotated vector $w$ to the original vector $n$.

Answer 1

As your question looks to be about alternative approaches, here is a straightforward one one using distances :

Principle : It is equivalent to say that 2 lines are images one of the other by a rotation with center $P_0$ and that these lines are at the same distances from $P_0$.

In a practical way : Let $d$ be the distance from the given line $(\ell)$ to the given point $P_0$.

It is known that the set of lines :

$$px+qy+r=0\tag{0}$$

tangent to the ellipse obeys the constraint :

$$\pmatrix{p&q&r}Q^{-1}\pmatrix{p\\q\\r}=0\tag{1}$$

Besides, we have the classical formula for the distance $d$ from a point $P_0 (x_0,y_0)$ to a straight line with equation (0) is :

$$d^2=\frac{(px_0+qy_0+r)^2}{p^2+q^2}\tag{2}$$

Besides, we can assume without loss of generality that equation (0) is "normalized" by condition :

$$p^2+q^2=1.\tag{3}$$

Solving system (1)+(2)+(3), we get the value(s) of $p,q,r$.

The last step, finding the angle of rotation is not difficult because one has just to determine the angles of directing vectors $v$ and $\binom{ \ \ q}{-p}$.

Answer 2

I created an example of an ellipse and a line that is to be rotated to become tangent to the ellipe. The ellipse is given by

$ \dfrac{(x - 6)^2}{5^2} + \dfrac{(y - 10)^2}{3^2} = 1 $

I then took $n = [0, 1]^T , r_0 = [2, 15]^T , P_0 = [-1, -3]^T $

The resulting solutions are shown below.

The angle of rotations, respectively, are $\theta_1 = -50.1073^\circ$ and $\theta_2 = -20.5004^\circ $